Most of my research involves trying to understand systems far-from-equilibrium
(meaning that the energy input and the energy dissipated are not precisely
balanced at all places and at all times). Unlike the situation for systems
in equilibrium, researchers have so far been stymied in their efforts to develop
a general, predictive theory of nonequilibrium systems. My research group uses
the tools of nonlinear dynamics and statistical physics to try to establish
the underpinnings for such a theory. Most of the work also involves the use
of large-scale computation, mostly on large computer clusters.
The types of systems I study range
from fluid and granular systems to electrochemical waves in heart tissue to
idealized mathematical models. Some of the projects are described below.
The work has been supported by the NSF, Research Corporation, NASA,
and the Sloan Foundation.
Dynamical Events in Spiral Defect Chaos
The behaviors of systems far-from-equilibrium can often appear hopelessly complicated
--- a muddled situation with a wide variety of length scales and time scales and often
a chaotic dynamics that defies prediction. We have been using the mathematical tools
of nonlinear dynamics to identify within this wild behavior particular events which
determine the future evolution of the system.
Using massively-parallel simulations of Rayleigh-Bénard convection, we found that
the complex behavior of the Spiral Defect Chaos state of convection is actually
largely determined by particular events (convection roll breaking) that are highly
localized in space and time. It is only in the vicinity of these events that the
system is particularly sensitive to small perturbations, so the rest
of the system, although complex-looking, is to a large degree predictable.
D.A. Egolf, I.V. Melnikov, W. Pesch, and R.E. Ecke, Nature 404:733-736 (2000).
|
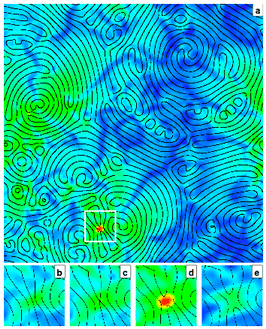 |
Jamming in Granular Shear
 |
Granular materials are collections of discrete, macroscopic particles
characterized by relatively straightforward interactions. Despite their
apparent simplicity, these systems exhibit a number of intriguing
phenomena, including the jamming transition, in which a disordered
collection of grains becomes rigid when its density exceeds a critical value.
We have been using dynamical analysis techniques to study the
behavior of a two-dimensional granular layer subjected to shear.
We have found that the transition from free-flowing states to jammed states is
a dynamical transition from chaotic behavior to non-chaotic behavior.
We also find that the dominant cooperative dynamical modes are strongly correlated
with particle rearrangements and become increasingly unstable before
stress jumps, providing a way to predict the times and locations of
these striking stress-release events.
In addition,
we have measured mathematically well-defined dynamical length scales and time
scales that diverge near the jamming transition density.
E.J. Banigan, M.K. Illich, D.J. Stace-Naughton, and D.A. Egolf,
Nat. Phys. 9:288-292 (2013).
|
Fibrillating Heart Tissue
We have been applying these same techniques to a model of fibrillating heart tissue,
with the hope of inspiring the development of targeted defibrillation in which tiny
electrical (or chemical) pulses can be introduced in specified portions of the heart
to lead the heart out of fibrillation in a gentle way. Again, we found that
particular events within the complicated chaotic dynamics of fibrillation largely
determine the future behavior of the fibrillating tissue. However, we found an
additional wrinkle that some events which initially appear to be extremely sensitive
to perturbations are quickly followed by periods of behavior that cancel
the effect of the sensitive period to a large degree.
|
 |
Building Blocks of Spatiotemporal Chaos
Such complicated behavior arising from isolated events provides hope
that we may be able to develop an understanding of these systems by characterizing
the events and the parts of the system involved in the events (much like the way
we can understand a great deal about gases by understanding atoms and the ways
they interact when they get close to each other). The idea that spatiotemporal chaotic
systems could be considered as a collection of weakly-interacting subsystems was
originally argued by Ruelle and later expanded upon by
Cross and Hohenberg and others. In a series of papers, we have explored this idea
in hopes of identifying these building blocks on which to base a statistical
mechanics of spatiotemporal chaos.
M.P. Fishman and D.A. Egolf, Phys. Rev. Lett. 96:054103 (2006).
D.A. Egolf, Phys. Rev. Lett. 81:4120-4123 (1998).
C.S. O'Hern, D.A. Egolf, and H.S. Greenside, Phys. Rev. E 53:3374-3386 (1996).
D.A. Egolf and H.S. Greenside, Phys. Rev. Lett. 74:1751-1754 (1995).
D.A. Egolf and H.S. Greenside, Nature 369:129-131 (1994).
|
 |
Statistical Mechanics Far-from-equilibrium
One of the reasons researchers are hopeful that a statistical mechanics of
spatiotemporal chaos might be developed is that the behavior of many of these systems
resembles the phase transitions of equilibrium systems. In a paper in Science
I showed that, remarkably, a coarse-graining of a simple spatiotemporal chaotic system
is indistinguishable from an equilibrium system of the Ising universality class.
D.A. Egolf, Science 287:101-104 (2000). |
 |
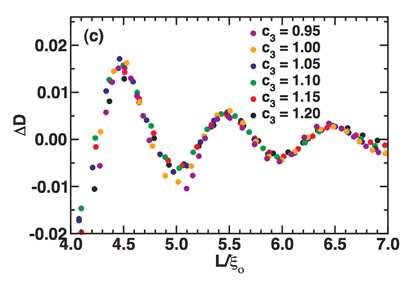
More Granular Dynamics
Since arriving at Georgetown, I have developed a successful collaboration with
Prof. Jeffrey Urbach
to study the thermodynamics of driven granular systems.
In a series of papers, we have described our efforts to understand the behavior
of these granular systems. In early work, we explored the relationship between
the way the system is driven and correlations within the granular media.
In more recent work, we studied two phenomena that appear in our non-equilibrium
granular systems and also in equilibrium systems --- two-phase coexistence and the
depletion force --- and characterized the similarities and differences between
the equilibrium and non-equilibrium situations. Our current work involves
driving a granular system using both shaking and shearing to introduce multiple
time-scales, and we're seeing some intriguing behavior.
P. Melby, A. Prevost, D.A. Egolf, and J.S. Urbach, Phys. Rev. E.
76:051307 (2007).
P. Melby, F.V. Reyes, A. Prevost, R. Robertson, P. Kumar, D.A. Egolf, and J.S. Urbach,
J. Phys. Cond. Matt. 17:S2689-S2704 (2005).
A. Prevost, P. Melby, D.A. Egolf, and J.S. Urbach, Phys. Rev. E 70:050301 (2004).
A. Prevost, D.A. Egolf, and J.S. Urbach, Phys. Rev. Lett. 89:084301 (2002).
Biophysics
My colleague Jeff Urbach and I have two students working on projects to study
the behavior of biopolymers in solution and in networks. This work will
hopefully give us insight into important mechanisms at work within cells.
QCD Calculations using Effective Field Theories
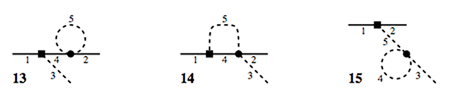
My scientific interests are quite broad, so I occasionally work on projects far
afield from my usual research. I have been working with
Professor Roxanne Springer
at Duke to calculate various quantities using effective theories of low energy
quantum chromodynamics (QCD). In our most recent work, we found that a
new 3-body force is required to describe the interactions of 3 nucleons
when 2 of them are charged (but that force is not needed when only one
is charged).
In earlier work, at the request of experimentalists at Fermilab,
we calculated the decay rates of doubly-heavy baryons into a variety of
channels.
J. Vanasse, D.A. Egolf, J. Kerin, S. Konig, and
R.P. Springer, Phys. Rev. C 89:064003 (2014).
D.A. Egolf, R.P. Springer, and J. Urban, Phys. Rev. D 68:013003 (2003).
D.A. Egolf, I.V. Melnikov, and R.P. Springer, Phys. Lett. B 451:267-274 (1999).
|