Interaction picture review

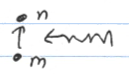
Our general interaction picture formalism showed \[\begin{aligned} & \left|\psi_{s}(t)\right\rangle=e^{-\frac{i}{\hbar} \hat{H}_{0}\left(t-t_{0}\right)} \hat{U}_{I}\left(t, t_{0}\right)\left|\psi_{s}\left(t_{0}\right)\right\rangle \\ & \hat{U}_{I}\left.(t,\left. t_{0}\right)=T e^{-\frac{i}{\hbar} \int_{t_{0}}^{t} \hat{V}_{I}\left(t^{\prime}\right) d t^{\prime}}=1-\frac{i}{\hbar} \int_{t_{0}}^{t} \hat{V}_{I}\left(t^{\prime}\right) d t^{\prime}+\left(\frac{-i}{\hbar}\right)^{2} \int_{t_{0}}^{t} d t_{1} \int_{t_{0}}^{t} d t_{2}\right. \hat{V}_I(t_1)\hat{V_I}(t_2) + \cdots \end{aligned}\] Then the probability to have a transition from state\(|i\rangle\) at \(t_0\) to state \(\langle f|\) at time \(t\) is \[P_{f \leftarrow i}(t)= \left| \langle f| e^{\frac{-i}{\hbar} \hat{H}_{0}\left(t-t_{0}\right)} \hat{U}_{I}(t,t_{0})|i\rangle\right|^{2}\]

If \(\langle f|\) and \(|i\rangle\) are eigenstates of \(\hat{H}_{0}\) then \(\langle f| e^{-\frac{i}{h} \hat{H}_{0}(t-t_0)}=e^{-\frac{i}{\hbar} E_{f}(t-t_0)}\langle f|\) is a phase whose modulus squared \(=1\), so \[\begin{aligned} P_{n \leftarrow m}(t)&=\left|{}_{0}\langle n| \hat{U}_{I}\left(t, t_{0}\right)| m\rangle_0\right|^{2} \\ &=\left|{}_0\langle n| \left (1-\frac{i}{\hbar} \int_{0}^{t} d t^{\prime} \hat{V}_{I}( t^{\prime})+\cdots\right )|m\rangle_{0}\right|^{2} \\ &=\left | \delta_{n m}-\frac{i}{\hbar} {}_{0}\langle n| \int_{t_{0}}^{t} e^{\frac{i}{\hbar} \hat{H}_{0}\left(t-\left.t_{0}\right)\right.} \hat{V}\left(t_{1}\right) e^{-\frac{i}{\hbar} \hat{H}\left(t_{1}-t_{0}\right)}|m\rangle_{0}+\cdots\right|^{2}. \end{aligned}\]

Perturbation theory

Define \(\omega_{nm}=\left(E_{n}^{0}-E_{m}^{0}\right) / \hbar\), then the lowest order approximation, called the first Born approximation is

\[\begin{aligned} P_{n \leftarrow m}(t) & \approx\left|\delta_{n m}-\frac{i}{\hbar} \int_{t_{0}}^{t} e^{i w_{n m}\left(t_{1}-t_{0}\right)} {}_0\langle n| \hat{V}(t_{1}) |m\rangle_0 dt_{1}\right|^{2} \\ & =\left|\delta_{n m}-\frac{i}{\hbar} \int_{t_{0}}^{t} d t_{1} e^{i w_{n m}\left(t_{1}-t_{0}\right)} V_{n m}\left(t_{1}\right)\right|^{2}. \end{aligned}\] So, if \(n \neq m\), we have that \[\boxed{ P_{\substack{n\leftarrow m \\n \neq m}}(t)=\frac{1}{\hbar^{2}}\left|\int_{t_{0}}^{t} d t_{1} e^{i w_{n m}\left(t_{1}-t_{0}\right)} V_{n m}\left(t_{1}\right)\right|^{2}}\]

Harmonic perturbation

When the potential takes the form \[\hat{V}(t)=e^{i \Omega t} \hat{a}^{\dagger}+e^{-i \Omega t} \hat{a}, \quad \Omega>0=\text { driving frequency and } \hat{a} \text{ is any operator}\] we have what is called a harmonic perturbation. Assume \(a_{n m}={ }_{0}\langle n| \hat{a}|m\rangle_{0} \neq 0\) and \(t_{0}=0\), then \[\begin{aligned} P_{\substack{n \leftarrow m \\ n \neq m}}(t) &=\frac{1}{\hbar^{2}}\left|\int_{0}^{t} d t_{1} e^{i w_{n m} t_{1}}\left(a_{n m} e^{-i \Omega t_{1}}+a_{n m}^{*} e^{i \Omega t_{1}}\right)\right|^{2} \\ & =\frac{1}{\hbar^{2}} \left\lvert\, \frac{a_{n m}}{i\left(w_{n m}-\Omega\right)}\left(e^{i\left(w_{n m}-\Omega\right) t}-1\right)+\frac{a_{n m}^{*}}{i\left(w_{n m}+\Omega\right)}\left(\left. e^{\left.i\left(w_{n m}+\Omega\right)t\right.}-1\right)\right|^{2}\right. \\ & =\frac{1}{\hbar^{2}}\left\{\frac{\left|a_{n m}\right|^{2}}{\left(w_{n m}-\Omega\right)^{2}} 2\left(1-\cos \left(w_{n m}-\Omega\right) t\right.) \right. \\ & \left.+\frac{\left|a_{n m}\right|^{2}}{\left(w_{n m}+\Omega\right)^{2}} 2\left(1-\cos \left(w_{n m} - \Omega \right) t\right)+\text { cross terms }\right\} \\ & =\frac{4}{\hbar^{2}} \left|a_{n m}\right|^{2}\left[ \frac{\sin ^{2}\left(w_{n m}-\Omega\right) \frac{t}{2}}{\left(w_{n m}-\Omega\right)^{2}}+\frac{\left.\sin ^{2} ( w_{n m}+\Omega\right) \frac{t}{2}}{\left(w_{n m}+\Omega\right)^{2}}+\cos \Omega\right] . \end{aligned}\] The first term is large if \(\omega_{mn}>0\) and \(\omega_{nm}\approx \Omega\), while the second term is large if \(\omega_{nm}<0\) and \(\omega_{nm}\approx-\Omega\). Both conditions are called resonance.

\[w_{nm} \rightarrow \Omega \qquad E_n = E_m + \hbar \Omega \qquad \text{stimulated absorption}\]

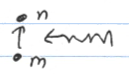
\[-w_{nm} \rightarrow \Omega \qquad E_n = E_m - \hbar \Omega \qquad \text{stimulated emission}\]

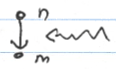
Accuracy: expect first Born to be accurate for \(P_{n \leftarrow m} \ll 1\). The worst case is on resonance where \(P_{n \leftarrow m} \sim c t^{2}\), which is larger than 1 for long enough time.
In general probabilities oscillate with time (recall cyclotron resonance problem)
The problem with first order perturbation theory is it neglects depletion and return
depletion: expect probability of \(P_{n \leftarrow m}\) to decrease when most m’s are gone
return: after n’s populated, they re-emit back to m.
Both processes are higher order effects.
Example: photo-ionization of Hydrogen - when a photon knocks an electron out of \(H\), little chance it will return back. In this case, neglecting return is OK.

Example of perturbation theory for an exactly solvable problem

Compare to the solvable example of last lecture.
Recall we showed \[\begin{aligned} |\psi_{s}(t)\rangle & = e^{i \omega t(\hat{a}^{\dagger} \hat{a} + \frac{1}{2})}\exp\left[-\frac{c}{\hbar (\Omega + \omega)}(e^{i(\omega + \Omega)t} -1)\hat{a}^{\dagger} + \frac{c}{\hbar (\Omega + \omega)}(e^{i(\omega + \Omega)t} -1)\hat{a}\right]\\ &*e^{i\frac{c^2}{\hbar^2(\Omega + \omega)^2}[(\omega + \Omega)t-\sin(\omega + \Omega)t]}|\psi_s(0)\rangle \end{aligned}\] for \(\hat{H}=\underbrace{\hbar \omega(\hat{a}+\hat{a}+\frac{1}{2})}_{\hat{H}_0}+\underbrace{c e^{i \Omega t} \hat{a}^{\dagger}+c e^{-i \Omega t} \hat{a}}_{\hat{V}} \qquad c \in \mathbb{R}\).
Consider the following operator identity: \[\begin{aligned} & e^{\tau(\hat{A}+\hat{B})} e^{-\tau \hat{B}} e^{-\tau \hat{A}}=f(\tau) \quad \text { with }[\hat{A}, \hat{B}]=\text { number } \\ & e^{\tau(\hat{A}+B)}(\hat{A}+\hat{B}) e^{-\tau \hat{B}} e^{-\tau A}-e^{\tau(A+B)} \hat{B} e^{-\tau \hat{B}} e^{-\tau \hat{A}}-e^{\tau(\hat{A}+\hat{B})} e^{-\tau \hat{B}} \hat{A} e^{-\tau \hat{A}} \\ & =\frac{d f(\tau)}{d \tau} \end{aligned}\] \[\begin{aligned} e^{\tau(\hat{A}+\hat{B})}\left[\hat{A}, e^{-\tau \hat{B}}\right] e^{-\tau \hat{A}}&=\frac{d f( \tau)}{d \tau}\\ \text{But } [\hat{A},e^{-\tau \hat{B}}] = \sum_{n=0}^\infty\frac{(-\tau)^n}{n!}[\hat{A},\hat{B}^n] &= \sum_{n=0}^{\infty}\frac{(-\tau)^n}{n!}[\hat{A},\hat{B}]\hat{B}^{n-1}n \text{ when } [\hat{A}, \hat{B}] = \text{number}\\ &= -\tau[\hat{A}, \hat{B}]e^{-\tau\hat{B}}\\ \text{so } \frac{df(\tau)}{d\tau} = \tau[\hat{B},\hat{A}]f(\tau) \Rightarrow f(\tau) &= e^{\frac{\tau^2}{2}[\hat{B},\hat{A}]}, \qquad \text{let } \tau =1\\ \text{or } e^{\hat{A}+\hat{B}} & = e^{\frac{1}{2}[\hat{B},\hat{A}]}e^{A}e^{B} \end{aligned}\] \[\begin{aligned} \text { apply to } \hat{A} & =\frac{-c}{\hbar(\omega+\Omega)}\left(e^{i(\omega+\Omega) t}-1\right) a^{\dagger} \\ \hat{B} & =\frac{c}{\hbar(\omega+\Omega)}\left(e^{-i(\omega+\Omega) t}-1\right) \hat{a} \\ {[\hat{B}, \hat{A}] } & =\frac{-c^{2}}{\hbar^{2}(\omega+\Omega)^{2}} 2(1-\cos (\omega+\Omega) t). \end{aligned}\] Thus, if we start in the ground state, we find \[\begin{aligned} P_{m \leftarrow 0}(t) & =\left| {}_0\langle m| e^{i \omega t (\hat{a}^{\dagger} \hat{a}+\frac{1}{2})} e^{-\frac{c}{\hbar(\omega+\Omega)}\left(e^{i(\omega+\Omega) t}-1\right) a^{\dagger}}\right. e^{\frac{c}{\hbar(\omega+\Omega)}\left(e^{-i(\omega+\Omega) t}-1\right) \hat{a}} |0\rangle_0 \\ & \times\left.e^{-\frac{c^{2}}{\bar{\hbar}^{2}(\omega+\Omega)^{2}}(1-\cos (\omega+\Omega) t)} e^{i \frac{c^{2}}{\hbar^{2}(\omega+\Omega)^{2}}((\omega+\Omega) t-\sin (\omega+\Omega) t)}\right|^{2} \\ & =e^{-\frac{2 c^{2}}{\hbar^{2}(\omega+\Omega)^{2}}(1-\cos (\omega+\Omega) t)}\left|{}_0\langle m| e^{-\frac{c}{\hbar(\omega+\Omega)}\left(e^{i(\omega+\Omega) t a^{2} t} -1\right)\hat{a}^{\dagger}}|0\rangle_{0}\right|^{2}. \end{aligned}\] But, \({}_0\langle m|={}_0 \langle 0| \frac{\left(\hat{a}\right)^{m}}{\sqrt{m!}}\) and \(e^{-\frac{c}{\hbar(\omega+\Omega}\left(e^{i(\omega+\Omega)t } -1\right)\hat{a}^{\dagger}} = \sum_{n=0}^{\infty}\left(-\frac{c}{\hbar(\omega \Omega)} (e^{i(\omega + \Omega)t}-1)\right)^n \frac{1}{n!}(\hat{a}^{\dagger})^n.\) We need \(n=m\) and \(\langle 0|\left(\hat{a}\right)^{m}\left(\hat{a}^{\dagger}\right)^{m}|0\rangle=m!\), so \[\begin{aligned} & P_{m \leftarrow 0}(t)=e^{-\frac{2 c^{2}}{\hbar^{2}(\omega+\Omega)^{2}} (1-\cos (\omega+\Omega)t)} \left[\frac{c^{2}}{\hbar^{2}(\omega+\Omega)^{2}}2(1-\cos (\omega+\Omega) t)\right]^{m} \frac{1}{m!} \\ & \boxed{P_{m \leftarrow 0}(t)=\frac{1}{m!}\left(\frac{2 c^{2}}{\hbar^{2}(\omega+\Omega)^{2}}\right)^{m}(1-\cos (\omega+\Omega) t)^{m} e^{-\frac{2 c^{2}}{\hbar^{2}(\omega+r)^{2}}(1-\cos (\omega+\Omega) t)}} \end{aligned}\] This is the exact solution.
One can directly check that \[\begin{aligned} & \sum_{m=0}^{\infty} \frac{1}{m!}\left(\frac{2 c^{2}}{\hbar^{2}(\omega+\Omega)^{2}}\right)^{m}(1-\cos (\omega+\Omega) t)^{m} e^{-\frac{2 c^{2}}{\hbar^{2}(\omega+\Omega)^{2}}(1-\cos (\omega+\Omega) t)} \\ & =\exp \left[\frac{2 c^{2}}{\hbar^{2}(\omega+\Omega)^{2}}(1-\cos (\omega+\Omega) t)-\frac{2 c^{2}}{\hbar^{2}(\omega+n)^{2}}(1-\cos (\omega+\Omega) t)\right] \\ & =1 \text { as it must. } \end{aligned}\]

Compare to the harmonic calculation \[\begin{aligned} &\langle m| c \hat{a}^{\dagger}|0\rangle=0 \text { unless } m=1 \\ &\langle m|\hat{a}^{\dagger} | 0\rangle=c \delta_{m 1} \quad \text{and}\quad \omega_{10} = \omega \\ & P_{1 \leftarrow 0}(t) \cong \frac{4 c^{2}}{\hbar^{2}} \frac{\sin ^{2}(\omega+\Omega) t^{\frac{1}{2}}}{(\omega + \Omega)^{2}}, \end{aligned}\] which agrees with the above form for \(m=1\) to lowest order in \(c^{2}\) when we note that \[1-\cos (\omega+\Omega) t=2 \sin ^{2}[(\omega+\Omega) t / 2].\]