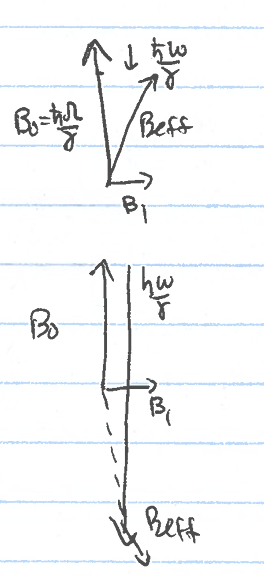
When we studied magnetic resonance, we found the Hamiltonian became \[\hat{H}_{\text{rot}} = -\hbar (\Omega - \omega) \hat{S}_z - \gamma B_1 \hat{S}_x\] in the rotating frame, with \(B_0 = \frac{\hbar \Omega}{\gamma}\) being the stationary field and \(B_1\) the rotating field at frequency \(\omega\). Thus, the spin sees a static field pointing in some direction which it precesses about: \[{B}_{\text{eff}} = \frac{\hbar (\Omega - \omega)}{\gamma} \hat{z} + B_1 \hat{x}.\] Suppose we start with the spin up and \(\omega \to 0\). As \(\omega \to 0\), \({B}_{\text{eff}}\) lies along the \(\hat{z}\) direction. As \(\omega\) increases, \({B}_{\text{eff}}\) rotates until it is in the \(-\hat{z}\) direction. If the spin precesses about the \({B}_{\text{eff}}\) axis as \(\omega\) is slowly increased, it goes from spin up as \(\omega \to 0\) to spin down as \(\omega \to \infty\).

Hence, the spin can flip by ramping \(\omega\) slowly. This type of flip of the spin is often studied as a \(2 \times 2\) problem called the Landau-Zener problem. Here, the Hamiltonian is given by: \[\hat{H}(t) = \begin{pmatrix} \delta t & V \\ V & -\delta t \end{pmatrix} = \delta t \sigma_z + V \sigma_x\] and is time-dependent. The instantaneous energy eigenvalues are: \[(\delta t - E)(-\delta t - E) - V^2 = 0\] which simplifies to \(E^2 = (\delta t)^2 + V^2\) or: \[E_\pm(t) = \pm \sqrt{(\delta t)^2 + V^2}.\] We can plot this as:
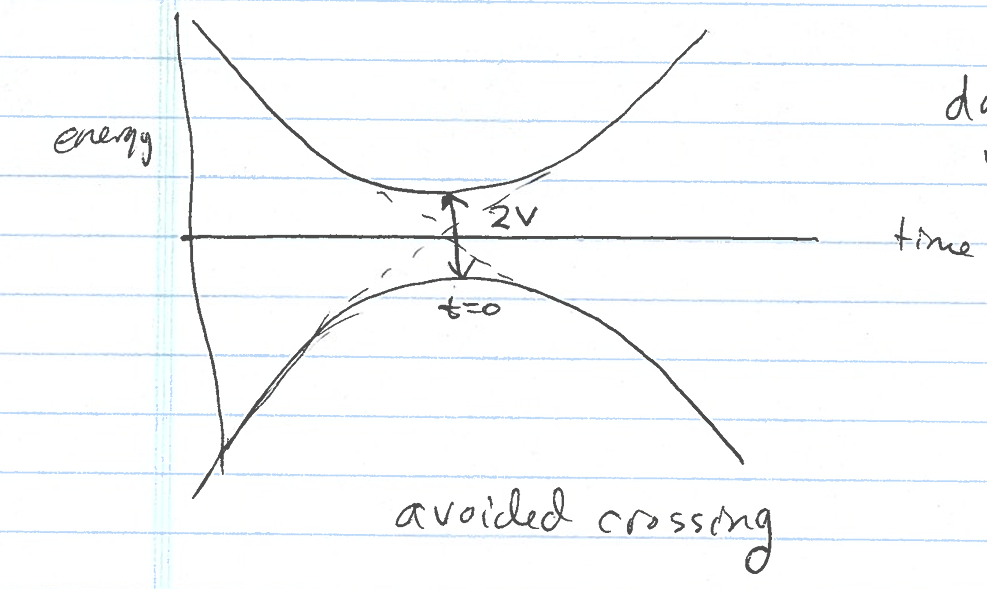
where the dashed line is for \(V=0\). The eigenfunctions can always be written in the following form: \[|+\rangle = \begin{pmatrix} \cos \frac{\theta}{2} \\ \sin \frac{\theta}{2} \end{pmatrix} \quad \text{and}\quad |-\rangle = \begin{pmatrix} \sin \frac{\theta}{2} \\ \cos \frac{\theta}{2} \end{pmatrix},\] where \(\theta\) is a function of time. These are the instantaneous eigenvectors. This form always holds since the states are orthonormal. To find \(\theta(t)\), we force the eigenvalue equation to work: \[\hat{H}(t)|+\rangle = E_+(t)|+\rangle,\] which gives: \[\delta t \cos \frac{\theta}{2} + V \sin \frac{\theta}{2} = \sqrt{(\delta t)^2 + V^2} \cos \frac{\theta}{2}.\] Simplifying, we obtain: \[\tan \frac{\theta}{2} = \frac{\sqrt{(\delta t)^2 + V^2} - \delta t}{V}.\] Using the trig identity \[\tan \theta = \tan \left(\frac{\theta}{2} + \frac{\theta}{2}\right) = \frac{\tan \frac{\theta}{2} + \tan \frac{\theta}{2}}{1 - \tan^2 \frac{\theta}{2}},\] We get: \[\begin{aligned} \tan \theta &= \frac{2 \sqrt{(\delta t)^2 + V^2} - \delta t}{V} \frac{1}{1 - \frac{\left (\sqrt{(\delta t)^2 + V^2} - \delta t\right)^2}{V^2}} \\ &=\frac{2 \sqrt{(\delta t)^2 + V^2} - \delta t}{V} \cdot \frac{V^2}{V^2 - \left((\delta t)^2 + V^2\right) - \delta t^2 + 2\delta t \sqrt{(\delta t)^2 + V^2}} \\ &=\frac{2V\sqrt{(\delta t)^2 + V^2} - \delta t}{2\delta t (\sqrt{(\delta t)^2 + V^2} - \delta t)}= \frac{V}{\delta t} \end{aligned}\] Thus, we get: \[\boxed{\tan \theta = \frac{V}{\delta t}.}\] Note that \(\theta = \pi\) at \(t \to -\infty\) and runs down to \(0\) at \(t \to \infty\). We also have that \(\frac{d\theta}{dt} < 0\) as shown below.
Now, recall our first attempt at time-dependent problems, in which we started with: \[\begin{aligned} |\psi(t)\rangle &= \sum_n c_n(t) |n(t)\rangle\\ \hat{H}(t)|n(t)\rangle &= E_n(t)|n(t)\rangle. \end{aligned}\] And hence, we get the time-dependent Schrödinger equation becomes: \[i\hbar \frac{\partial}{\partial t} |\psi(t)\rangle = \sum_n \left( i\hbar \frac{dc_n(t)}{dt} |n(t)\rangle + i\hbar c_n(t) \frac{\partial |n(t)\rangle}{\partial t} \right)= \hat{H}(t)|\psi(t)\rangle = \sum_n c_n(t) E_n(t) |n(t)\rangle\] Let: \[c_n(t) = \alpha_n(t) \exp\left[-\frac{i}{\hbar} \int^t E_n(t') \, dt'\right].\] The phase in the exponential is called the dynamical phase. Then, taking the derivative, we find: \[i\hbar \frac{d}{dt} c_n(t) = i\hbar \frac{d}{dt} \alpha_n(t) e^{-\frac{i}{\hbar} \int^t E_n(t') \, dt'} + \alpha_n(t) e^{-\frac{i}{\hbar} \int^t E_n(t') \, dt'} E_n(t)\] and we get: \[i\hbar \sum_n \left[\frac{d}{dt} \alpha_n(t) e^{-\frac{i}{\hbar} \int^t E_n(t') \, dt'} |n(t)\rangle + \alpha_n(t) e^{-\frac{i}{\hbar} \int^t E_n(t') \, dt'} \frac{\partial |n(t)\rangle}{\partial t} \right] = 0.\] Multiplying by \(\langle m(t)|\exp(\tfrac{i}{\hbar}\int^tE_m(t')dt')\), we obtain: \[\frac{d}{dt} \alpha_m(t) = -\sum_{n\ne m} \alpha_n(t) e^{-\frac{i}{\hbar} \int^t \left(E_n(t') - E_m(t')\right) dt'} \frac{\langle m(t)| \frac{\partial}{\partial t} |n(t)\rangle}{i\hbar}.\] For us, we assume the system starts in the lowest energy state \(|-\rangle\). If the ramping \(\delta\to0\) in time is slow, the state essentially remains in \(|-\rangle\) with the probability of it being in \(|+\rangle\) being very small. Hence, \(\alpha_{-}(t) \sim 1\) and \(\alpha_{+}(-\infty) = 0\). The above equation gives (after integrating): \[\alpha_{+}(\infty) = - \int_{-\infty}^{\infty} dt \, \alpha_{-}(t) e^{\frac{i}{\hbar} \int^{t} (E_{-}(t') - E_{+}(t')) dt'} \langle+ | \frac{\partial}{\partial t} | -\rangle\] Since \(\langle - | \frac{\partial}{\partial t} | -\rangle= 0\) as we now show: \[\begin{aligned} \frac{\partial}{\partial t} |+\rangle &= -\frac{d\theta}{dt} \frac{1}{2} \begin{pmatrix} \sin \frac{\theta}{2} \\ -\cos \frac{\theta}{2} \end{pmatrix} = -\frac{1}{2} \frac{d\theta}{dt} |-\rangle \\ \frac{\partial}{\partial t} |-\rangle &= \frac{d\theta}{dt} \frac{1}{2} \begin{pmatrix} \cos \frac{\theta}{2} \\ \sin \frac{\theta}{2} \end{pmatrix} = \frac{1}{2} \frac{d\theta}{dt} |+\rangle. \end{aligned}\] Thus: \[\begin{cases} \langle- | \frac{\partial}{\partial t} | -\rangle = \langle+ | \frac{\partial}{\partial t} | +\rangle= 0 \\ \langle+ | \frac{\partial}{\partial t} | -\rangle =\frac{1}{2} \frac{d\theta}{dt} \\ \langle- | \frac{\partial}{\partial t} | +\rangle = -\frac{1}{2} \frac{d\theta}{dt}. \end{cases}\] Therefore: \[\alpha_{+}(\infty) \sim -\frac{1}{2} \int_{-\infty}^{\infty} dt \frac{d\theta}{dt} e^{\frac{2i}{\hbar} \int^{t} \sqrt{(\delta t')^2 + V^2} dt'}.\] Now recall the equation \(\tan \theta(t) = \frac{V}{\delta t}\) and rearrange it to get \(\sec^2 \theta \frac{d\theta}{dt} = -\frac{V}{(\delta t^2)}\) and solve for \(d\theta/dt\) to get: \[\frac{d\theta}{dt} = -\frac{V}{\delta t^2} \frac{1}{1 + \left(\frac{V}{\delta t}\right)^2} = -\frac{V \delta }{(\delta t)^2 + V^2}\] Plugging this for our formula for \(a_+(\infty)\), we get: \[\boxed{\alpha_{+}(\infty) \sim \frac{1}{2} \int_{0}^{\infty} dt \frac{V \delta}{(\delta t)^2 + V^2} e^{\frac{2i}{\hbar} \int^{t} \sqrt{(\delta t')^2 + V^2} dt'}}.\] One can evaluate this using complex analysis to give: \[\alpha_{+}(\infty) \sim \frac{\pi}{3} e^{-\pi V^2 / \delta}\] or: \[P(t) = |\alpha_{+}(\infty)|^2 = \frac{\pi^2}{9} e^{-\pi V^2 / \delta}\] Note however that this result is only approximate. The correct answer, worked out by Zener using parabolic cylinder functions which solve Weber’s equation, yields: \[P(t) = e^{-\pi V^2 / \delta}\]
This holds for all \(\delta\), not just in the limit \(\delta \to 0\). So as \(\delta\) is made large, the probability to not flip the spin grows. Further note that this is a nonperturbative result in \(\delta\), so regular time-dependent perturbation theory will not work well. This is essentially because the time-dependent piece of \(H(t)\) varies from very large to very small and is not always small. In pictures we have:
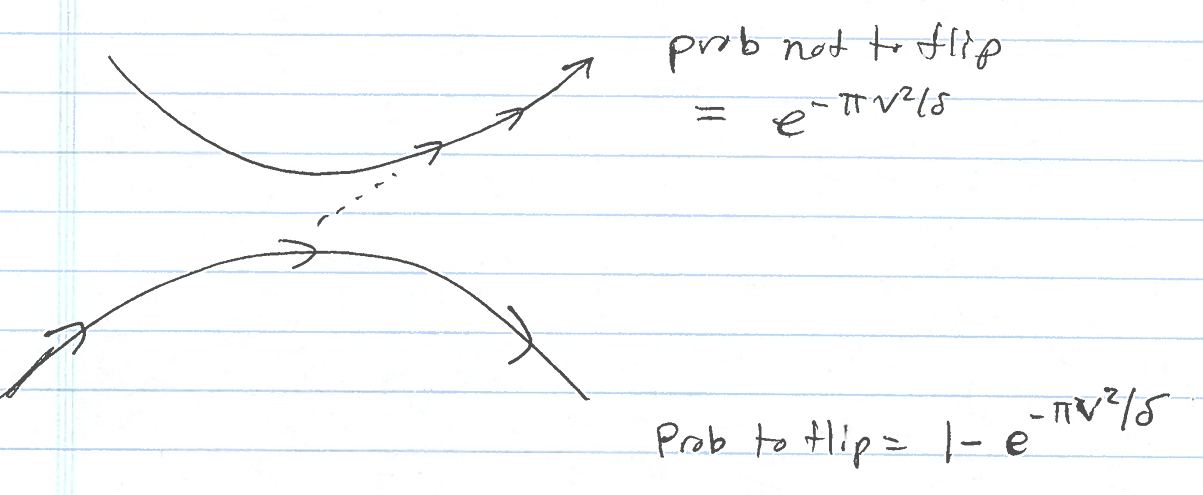
For the adiabatic limit, \(\delta\to0\) and we always flip. For the diabatic limit, \(\delta\to\infty\) and we never flip. The true case is somewhere in between.
One can also solve the problem numerically, but it has a number of challenges. One needs to evolve over an infinite time range, and the result has significant oscillations that are very slow to damp. Using a combination of ideas can allow you to get accurate results.