When we discussed time-dependent perturbation theory, we found the probability for a transition form state \(m\) to state \(n\) in the first Born approximation was \[P_{n\leftarrow m}(t)=\frac{1}{\hbar^{2}}\left|\int_{t_{0}}^{t} d t_{1} e^{i \omega_{n m}\left(t_{1}-t_{0}\right)}V_{n m}\left(t_{1}\right)\right|^{2}\] If \(\hat{V}\) is independent of time and \(t_0=0\), we have
\[P_{n \leftarrow m}(t)=\frac{4 \sin ^{2}\left(\frac{\omega_{n m }t}{2}\right)}{\hbar^{2} \omega_{n m}^{2}}\left|V_{n m}\right|^{2}.\]
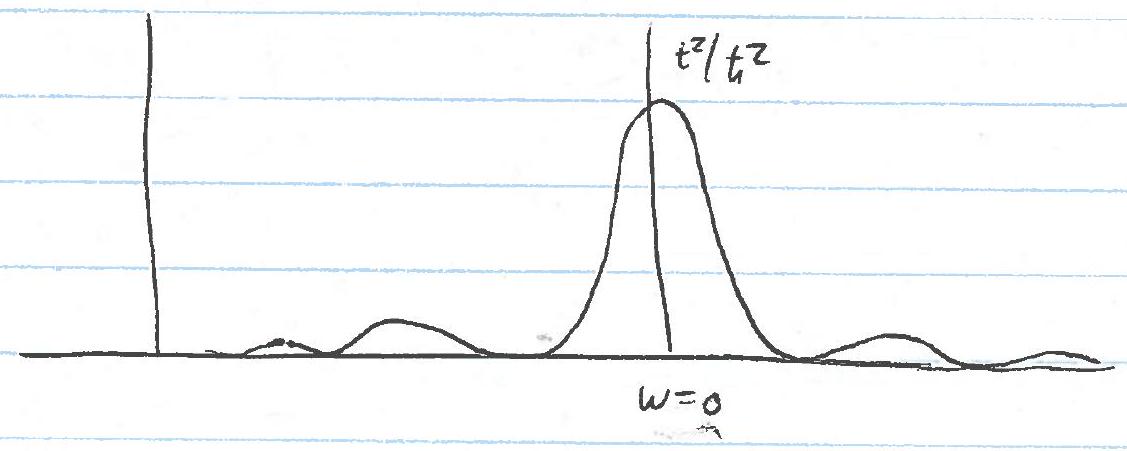
This is the result for a discrete spectrum. Consider generalizing to a continuous spectrum and plot the transition probability as a function of the "energy" \(\omega\). \[f(\omega)=\frac{4 \sin ^{2} \frac{\omega t}{z}}{\hbar^{2} \omega^{2}}\]

It is always positive. Furthermore, as \(t \rightarrow \infty \quad \text{we have}\quad f(\omega) \rightarrow c t \delta(\omega).\) But \(\int_{-\infty}^{+\infty} d \omega f(\omega) d \omega=\frac{2 \pi t}{\hbar^{2}} \Rightarrow c=\frac{2 \pi}{\hbar^{2}}.\) So, \(\lim _{t \rightarrow \infty} P_{n \leftarrow m}(t) \rightarrow \frac{\left|V_{n m}\right|^{2}}{\hbar^{2}} 2 \pi t \delta\left(\frac{E_{n}^{(0)}-E_{n}^{(0)}}{\hbar}\right)=\frac{2 \pi}{\hbar} t \delta\left(E_{n}^{(0)}-E_{m}^{(0)}\right)\left|V_{n m}\right|^{2}.\)
The rate at which \(P\)
increases is then \[\frac{d P_{n \leftarrow
m}(t)}{d t}=\dot{P}_{n \leftarrow m}(t)=\frac{2 \pi}{\hbar}
\delta\left(E_{n}^{0}-E_{m}^{(0)}\right)\left|V_{n
m}\right|^{2}.\] In the continuum, all energy levels are allowed,
so we drop the superscript (0).
Let \(n=f=\text{final} \quad \text{and}\quad
m=i=\text{initial}\), to get \[\boxed{
\dot{P}_{f \leftarrow i}(t)=\frac{2 \pi}{\hbar}
\delta\left(E_{f}-E_{i}\right)\left|V_{f i}\right|^{2}}\] called
Fermi’s Golden Rue (actually derived by Dirac).
In order to solve the depletion problem, we sometimes add an extra
factor of \(P\) on the RHS since the
rate should be proportional to the number of states. \[\dot{P}_{f \leftarrow i}(t)=\frac{2 \pi}{\hbar}
\delta\left(E_{f}-E_{i}\right)\left|V_{f i}\right|^{2} P(t)\] In
this case, the probability will always be bounded.
Example: Consider a Helium-like atom \((z=2)\) with a muon and an electron
orbiting it.
\[\text{electron} \quad (r, p, m) \quad
\text{and}\quad\text{muon}\quad (R, P, M) \quad \text{for}\quad M \gg
m:\] \[\hat{H}=\frac{\hat{p}^{2}}{2
m}-\frac{z e^{2}}{\hat{r}}+\frac{\hat{p}^{2}}{2 M}-\frac{z
e^{2}}{\hat{R}}+\frac{e^{2}}{|\mathbf{R}-\mathbf{r}|}\]
Since \(M \gg m\), the muon orbits
close to the nucleus, \(\Rightarrow\)
electron sees effective charge \(z_{\text{eff}}=1\).
Write \(\hat{H}=\hat{H}_{0}+\hat{V}\)
\[=\underbrace{\frac{\hat{p}^{2}}{2
m}-\frac{e^{2}}{\hat{r}}+\frac{\hat{P}^{2}}{2 M}-\frac{2
e^{2}}{\hat{R}}}_{H_{0}}+\underbrace{\frac{e^{2}}{|\mathbf{\hat{R}}-\mathbf{\hat{r}}|}-\frac{e^{2}}{\hat{r}}}_{V}.\]
Unperturbed wavefunctions are electron in \(H\) field and muon in the field. \[\begin{aligned} H_{0}|\psi(r, R)\rangle&=E(\Psi(r, R)\rangle\\ |\psi(r,R)\rangle_{nlm;n^{\prime}l^{\prime}m^{\prime}} &= \underbrace{U_{n^{\prime}l^{\prime}m^{\prime}}(R)}_{\text{Helium field}}\underbrace{u_{nlm}(r)}_{\text{Hydrogen field}} \end{aligned}\] \[E_{n n^{\prime}}=-\frac{m e^{4}}{2 \hbar^{2} n^{2}}-\frac{2 M e^{4}}{\hbar^{2} a^{12}}\] \[\begin{aligned} \text{ground state} \qquad n=n^{\prime}=1 \qquad E_{\text{gs}}=-\frac{e^4}{2\hbar ^2}[m + 4M]\\ \text{excited state} \qquad n=1 , n^{\prime}=2 \qquad E_{12}=-\frac{e^4}{2\hbar ^2}[m + M]\\ \end{aligned}\] \[E_{12}-E_{\text{gs}}=\frac{3 M e^{4}}{2 \hbar^{2}}.\]
Suppose the system starts in the excited state and drops to G.S. if the electron absorbs this energy (instead of a photon taking it away), its energy is \[\frac{e^{4}}{2 \hbar^{2}}[-m+3 M] \gg 0\] \(\Rightarrow\) the electron goes to the continuum and is ejected (like a so-called Auger transition).
Suppose at time \(t=0\) we are in the state \(n^{\prime} = 2 \quad n=1\). What is the electron ejection rate at large \(t\) ? You may assume that the emitted electron is a free particle, because it is a high-energy state. \[\begin{aligned} & \text { Rate }=\frac{2 \pi}{\hbar}\left|V_{f i}\right|^{2} \delta\left(E_{f}-E_{i}\right) \\ & E_{i}=-\frac{e^{4}}{2 \hbar^{2}}[M+m] \qquad E_{f}=-\frac{e^{4}}{2 \hbar^{2}}\left[4 M\right]+\frac{\hbar^{2} k^{2}}{2 m^{2}} \\ &|\psi_i\rangle = U_{2lm_l}(R)U_{100}(r)\\ &|\psi_f\rangle = U_{100}(R)e^{ik\cdot r}. \end{aligned}\]
Sum over all final momenta to get the total rate \[\sum_{k} \rightarrow \frac{1}{(2 \pi)^{3}} \int d^{3} k\] \[\begin{aligned} \text { Rate }&=\int \frac{d^{3} k}{(2 \pi)^{3}} \frac{2 \pi}{\hbar}\left|V_{f{i}}(k)\right|^{2} \delta\left(E_{f}-E_{i}\right) \\ d^{3} k&=k^{2} d k d \Omega=k \frac{d k^{2}}{2} d \Omega \quad \text{and}\quad \varepsilon_{k}=\frac{\hbar^{2} k^{2}}{2 m} \\ & =\left(\frac{2 m \varepsilon_{k}}{\hbar^{2}}\right)^{1 / 2} \frac{m}{\hbar^{2}} d \varepsilon_{k} d \Omega \quad\text{and}\quad d \varepsilon_{k}=d \varepsilon_{f} \\ \end{aligned}\]
\[\begin{aligned} R & =\int \frac{d \varepsilon_{f}}{(2 a)^{3}} d \Omega\left(\frac{2 m \varepsilon_ k}{\hbar^{2}}\right)^{1 / 2} \frac{m}{\hbar^{2}} (-\frac{2 \pi}{\hbar}) | V_{f i}(k) |^{2} \delta\left(E_{f}-E_{i}\right) \\ & =\int \frac{ d \Omega}{(2 \pi)^{3}}\left(\frac{2 m \frac{e^{4}}{2 \hbar^{2}}(3 M-m)}{\hbar^{2}}\right)^{1 / 2} \frac{m}{\hbar^{2}} \frac{2 \pi}{\hbar}\left|V_{f i}(\mathbf{k})\right|^{2} \\ & =\frac{1}{(2 \pi)^{2}\hbar^5} e^{2} m \sqrt{m(3 M-m)} \int d \Omega\left|V_{f i}(\mathbf{k})\right|^{2} \\ \left|V_{f{i}}(k)\right|^{2} & =\int d^{3} R \quad U_{2 l m_{l}}(R) U_{100}(R) \int d^{3} r e^{-i k \cdot r} U_{100}(r) \times \left[\frac{e^2}{|\mathbf{R} - \mathbf{r}|}- \frac{e^2}{r}\right] . \end{aligned}\]
Now we consider the sudden approximation.
Suppose the system is in a given time independent potential for \(t < 0\). At \(t=0\). The potential suddenly changes to a
new potential, which remains for all \(t >
0\). What happens to the states of the quantum system?
In practice, no potential changes instantly but these changes can be
very fast (like in radioactive decay). In these cases the sudden
approximation is valid.
Strategy - find the eigenfunctions of \(H(t<0)=\left|\psi_{i}\right\rangle\) and
of \(\bar{H}(t
>0)=\left|\psi_{f}\right\rangle\). The probability to find the
system in one of the \(f\) states given
that it started in an \(i\) state is
just the overlap: \[P_{f \leftarrow
i}=\left|\left\langle\psi_{f}|
\psi_{i}\right\rangle\right|^{2}.\] It is that simple.
Example: particle on a box of length \(L\). Assume it starts in the ground
state
At \(t=0\) the box increases in size to
\(2 L\). What is the probability to be
in each of the eigenstates of the wider box?
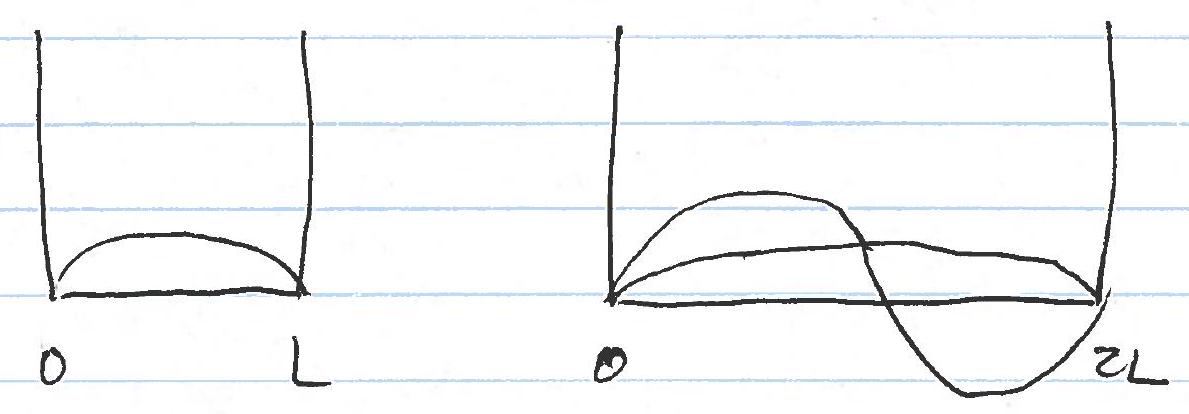
The wavefunctions for a particle in a box are \[\begin{aligned} \left|\psi_{n}\right\rangle & =\sqrt{\frac{2}{L}} \sin \frac{n \pi x}{L} & & n=1,2, \cdots \\ \text{so }\left|\psi_{i}\right\rangle & =\sqrt{\frac{2}{L}} \sin \frac{\pi x}{L} & & 0<x<L \\ & =0 & & x>L \\ \mid \psi_{f}(n)\rangle & =\frac{1}{\sqrt{L}} \sin \frac{n \pi x}{2 L} & & n=1,2, \ldots \end{aligned}\] \[\begin{aligned} P_{f \leftarrow i}&=\left|\left\langle\psi_{f}(n) \mid \psi_{i}\right\rangle\right|^{2}\\ &=\left|\int_{0}^{L} d x \sqrt{\frac{2}{L}} \sin \frac{\pi x}{L} \sqrt{\frac{1}{L}} \sin \frac{n \pi x}{2 L}\right|^{2}\\ &=\frac{2}{L^{2}}\left|\int_{0}^{L} d x \frac{1}{2}\left(\cos \frac{(n+2) \pi x}{2 L}-\cos \frac{(n-2) \pi x}{2 L}\right)\right|^{2}\\ &=\frac{1}{2 L^{2}}\left|\left[\frac{2 L}{(n+2) \pi} \sin \frac{(n+2) \pi x}{2 L}-\frac{2 L}{(n-2) \pi} \sin \frac{(n-2) \pi x}{2 L}\right]_{0}^{L}\right|^{2}\\ &=\frac{2}{\pi^{2}}\left|\sin \frac{(n+2) \pi}{2} \frac{1}{(n+2)}-\sin \frac{(n-2) \pi}{2} \frac{1}{(n-2)}\right|^{2} \end{aligned}\] \[=\left[\begin{array}{l} 0 \qquad n=\text{even}, n \neq 2 \\ \frac{1}{2} \qquad n = 2 \\ 32 /\left(\pi^{2}(n+2)^{2}(n-2)^{2}\right) \quad n=\text{odd}. \end{array}\right.\] Note that \[\begin{aligned} \sum_{n}\left|\left\langle\psi_{f}(n) \mid \psi_{i}\right\rangle\right|^{2}&=\underbrace{\frac{1}{2}}_{n=2}+\frac{32}{\pi^{2}} \sum_{n=0}^{\infty} \frac{1}{(2 n+3)^{2}(2 n-1)^{2}} \\ &= \frac{1}{2}+\frac{32}{\pi^{2}} \sum_{n=0}^{\infty}\left[\frac{1}{(2 n+3)^{2}}-\frac{1}{(2 n-1)^{2}}\right] \frac{1}{(-8)(2 n+1)} \\ &= \frac{1}{2}+\frac{4}{\pi^{2}} \sum_{n=0}^{\infty}\left(\frac{1}{(2 n-1)^{2}(2 n+1)}-\frac{1}{(2 n+3)^{2}(2 n+1)}\right) \\ &= \frac{1}{2}+\frac{4}{\pi^{2}} \sum_{n=0}^{\infty}\left\{\frac{1}{(2 n-1)}\left(\frac{1}{(2 n-1)}-\frac{1}{2 n+1}\right) \frac{1}{2}\right. \\ &\qquad \left.-\frac{1}{(2 n+3)}\left(\frac{1}{(2 n+1)}-\frac{1}{2 n+3}\right) \frac{1}{2}\right\} \\ &= \frac{1}{2}+\frac{2}{\pi^{2}}\sum_{n=0}^{\infty}\left\{\frac{1}{(2 n-1)^{2}}+\frac{1}{(2 n+3)^{2}}+\left(\frac{1}{(2 n-1)}-\frac{1}{2 n+1}\right)\left(-\frac{1}{2}\right)\right. \\ & \qquad \left.+\left(\frac{1}{(2 n+1)}-\frac{1}{2 n+3}\right) \left(-\frac{1}{2}\right)\right\}\\ &=\left.\frac{1}{2}+\frac{2}{\pi^{2}} \sum_{n=0}^{\infty}\left\{\frac{1}{(2n+1)^2}-\frac{1}{2(2 n-1)}\right)+ \frac{1}{2}\frac{1}{2n+3}\right\} \\ &\left.=\frac{1}{2}+\frac{4}{\pi^{2}} \cdot \frac{\pi^{2}}{8}=\frac{1}{2}+\frac{1}{2}=1\right. \end{aligned}\]
so \(\sum_{f} P_{f \leftarrow i}=1\) as it must!