Strongly correlated nanostructures

In this project, we are developing a many-body physics computational engine to determine the self-consistent solution of a multilayered device constructed of semi-infinite leads and a barrier region. We describe the barrier with the Falicov-Kimball model which can be tuned through a metal-insulator transition. We include the possibility of charge redistribution at the interfaces, magnetic spin polarization, Friedel oscillations, and so on. Once converged, we have the inhomogeneous many-body density of states and we can use that to calculate the Kubo (linear) response. In addition, we are developing a nonequilibrium formalism that will be exact for the many-body problem, and can be applied both to bulk and inhomogeneous systems. Finally we are comparing how Landauer-based approaches compare with the full many-body theory.

Our plan is to examine spintronic devices where some of the materials in the device have magnetic properties (typically ferromagnets), and to investigate thermoelectric coolers, composed out of heavy Fermions and either Mott or Kondo insulators.

Annotated list of publications

Nonequilibrium formalism

J. K. Freericks, V. M. Turkowski, and V. Zlatic', Nonequilibrium dynamical mean-field theory, submitted to Phys. Rev. Lett.
This work represents the first full many-body treatment of Bloch oscillations. We show how they evolve from a noninteracting system into a Mott insulator, where the damped oscillations become irregular in shape.
J. K. Freericks and V. Zlatic', Nonlinear Peltier effect and the nonequilibrium Jonson-Mahan theorem, Cond. Matter Phys. 9, 603--617 (2006).
The problem of the relationship between charge and heat currents is generalized from the linear-response to the nonlinear response regime. The Jonson-Mahan theorem can be generalized for part of the heat current, but there is an additional term related to Joule heating that is not easily evaluated.
J. K. Freericks, V. M. Turkowski, and V. Zlatic', Nonlinear response of strongly correlated materials to large electric fields, in Proceedings of the HPCMP Users Group Conference 2006, Denver, CO, June 26--29, 2006 edited by D. E. Post (IEEE Computer Society, Los Alamitos, CA, 2006).
Here we present a careful numerical error analysis of the accuracy of transient nonequilibrium calculations, whose physical results are summarized elsewhere. We also summarize how to efficiently parallelize the calculations.<\i><\li>
V. Turkowski and J. K. Freericks, Spectral moment sum rules for strongly correlated electrons in time-dependent electric fields, Phys. Rev. B 73, 075108--1-15 (2006).
This work generalizes a paper by Steve White on the spectral moments of the Hubbard model to the nonequilibrium case. We find that most spectral moment sum rules maintain essentially the same form as a field is turned on. The exact moments are compared to a number of numerical calculations to gauge the accuracy of the numerics.

V. Turkowski and J. K. Freericks, Nonlinear response of Bloch electrons in infinite dimensions, Phys. Rev. B 71, 085104--1-11 (2005).
In this article we solve for the noninteracting Green's functions of Bloch electrons in infinite dimensions. The solutions contain Bloch oscillations, as expected, They also form the building blocks for a many-body formalism for nonlinear and nonequilibrium response.

J. K. Freericks, V. O. Turkowski, and V. Zlatic', Real-time formalism for studying the nonlinear response of "smart" materials to an electric field, in Proceedings of the Users Group Conference Nashville, TN, June 28--30, 2005 (IEEE Computer Society, Los Alamitos, CA, 2005).
Here we test the full many-body nonequilibrium algorithm in real time against equilibrium results and we show how Bloch oscillations are damped as the correlations are increased.

J. K. Freericks and V. M. Turkowski, Steady state nonequilibrium dynamical mean-field theory and the quantum Boltzmann equation, J. Phys.: Confer. Ser. 35, 39--52 (2006). (Workshop on Progress in nonequilibrium physics III, Kiel, Germany, August, 2005).
In this work we explicitly show the equivalence of the Kubo formula for charge transport and the linear-response limit of the quantum Boltzmann equation derived from nonequilibrium Keldysh formalism.

J. K. Freericks, V. Turkowski, and V. Zlatic', F-electron spectral function of the Falicov-Kimball model in infinite dimensions: The half-filled case, Phys. Rev. B.

J. K. Freericks, V. O. Turkowski, and V. Zlatic', Parallelizing the Keldysh formalism for strongly correlated electrons, in Proceedings of the Users Group Conference, Willaimsburg, VA, June 7--11, 2004 (IEEE Computer Society, Los Alamitos, CA, 2004) p. 7--16.

J. K. Freericks, V. O. Turkowski, and V. Zlatic', F-electron spectral function near a quantum critical point, (proceedings of the Strongly Correlated Electron Systems conference, Karlsruhe, Germany), Physica B 359--361C, 684--686 (2005).
In this series of articles, we determine the equilibrium density of states in the bulk for the local electrons of the Falicov-Kimball model. This problem requires the use of a Kadanoff-Baym nonequilibrium formalism to carry out the analytic continuation, and serves as the simplest nontrivial problem that can be treated with the nonequilibrium approach. The numerical solution has a number of subtleties, which we believe will enter in the solution of the nonequilibrium problem for the conduction electrons.

Equilibrium formalism for nanostructures

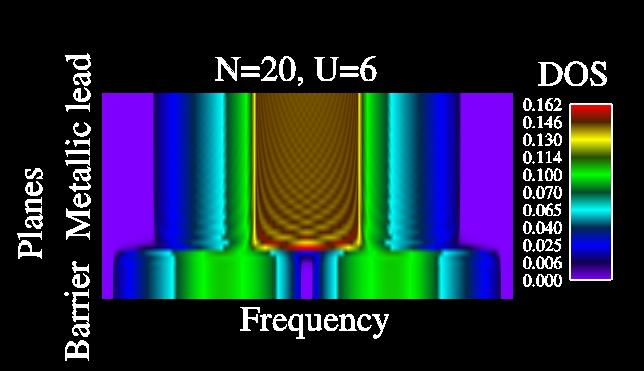
J. K. Freericks, Transport in multilayered nanostructures: the dynamical mean-field theory approach (Imperial College Press, London, 2006) 344 pages.
This is a comprehensive book that summarizes all of our work with inhomogeneous dynamical mean-field theory as applied to transport in multilayered devices (tunnel junctions, Josephson junctions, thermoelectric devices).

J. K. Freericks, V. Zlatic', and A. M. Shvaika, Electronic thermal transport in strongly correlated multilayered nanostructures, submitted to Phys. Rev. B.
This work shows how one can generalize the Jonson-Mahan theorem for the linear-response thermal transport from the bulk to a multilayered nanostructure.
J. K. Freericks and V. Zlatic', Enhancement of thermoelectric performance in strongly correlated multilayered nanostructures, (proceedings of the 30th international conference in theoretical physics, Ustron, Poland, 2006) submitted to phys. stat. sol. b (2006).
This work applies the theory developed above to particle-hole symmetric metals and Mott insulators that have a chemical potential mismatch. The electronic charge reconstruction that results creates substantial thermoelectric response, and can create electronic ZT values well in excess of 1.

J. K. Freericks Dynamical mean field theory for strongly correlated inhomogeneous multilayered nanostructures, Phys. Rev. B 70, 195342--1-14 (2004).

J. K. Freericks, Crossover from tunneling to incoherent (bulk) transport in a correlated nanostructure, Appl. Phys. Lett. 84, 1383--1385 (2004); Virtual Journal of Nanoscale Science and Technology, 9, Issue 8 (2004); Virtual Journal of Applications of Superconductivity, 6, Issue 5 (2004).

J. K. Freericks, Strongly correlated multilayered nanostructures near the Mott transition, (proceedings of the 24th international conference in theoretical physics, Ustron, Poland, 2004) phys. stat. sol. b 242, 189--195 (2005).
In this series of articles we show two key results. The first, is that there is a generalization of the Thouless energy, which can be thought of as an energy scale extracted from the resistance and the density of states of the barrier region, that describes the crossover from tunneling to incoherent (Ohmic) transport. The second, is that there is very small dependence of the self consistency on the thickness of the barrier, which implies that Landauer-based approaches, which assume the leads are unchanged by the thickness of the barrier, could be quite accurate in describing these systems if the correct barrier height is chosen.

Last modified January 12, 2005.

Jim Freericks, Professor of Physics, freericks@physics.georgetown.edu