Block copolymers are made by `gluing' chemically different polymer species,
say red and blue, together. A melt of these molecules will disorder at
high temperature due to entropic effects; however, at low temperatures
any net repulsive potential will induce them to separate. They would like
to separate into macroscopic regimes of blue and red, but cannot because
they are chemically bonded together. Instead, they separate as far as they
can, into various shaped domains which reflect the chemical asymmetry of
the block-copolymer.
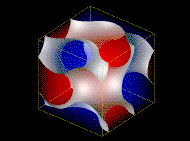
A symmetric molecule separates into stripes (lamellae) of red and blue, while a molecule with more blue than red separates into cylinders of red embedded in a matrix of blue (micelles), or spheres or, depending on how asymmetric the molecule is, any number (so it seems!) of exotic bicontinuous phases, such as the Gyroid phase pictured here (the observant reader will notice that this is not the actual gyroid phase: if you want to know what's wrong with this picture email me). For a good page devoted to minimal surfaces like this Gyroid phases, see Robert Holyst's Research Group. There is a wealth of interesting physics here, including the crystallography of these phases, molecular and collective fluctuation effects near the order-disorder transition and elsewhere, and the behavior under flow.
We consider micro- and macro- phase separation in blends of AB and BC diblock copolymers. We show that, depending on architecture, a number of phase diagram topologies are possible. Microphase separation or macrophase separation can occur, and there are a variety of possible Lifshitz points. Because of the rich parameter space, Lifshitz points of multiple order are possible. We demonstrate Lifshitz points of first and second order, and argue that, in principle, up to 5th order Lifshitz points are possible.
Strong-Segregation Theory of Bicontinuous Phases in Block Copolymers
PD Olmsted and ST Milner,
Macromolecules 31 (1998) 4011-4022
(abstract ,
reprint in .ps
or .pdf format).
We compute phase diagrams for diblock star copolymers in the strong-segregation regime as a function of volume fraction $\phi$, including bicontinuous phases related to minimal surfaces (G, D, and P surfaces) as candidate structures. We present the details of a general method to compute free energies in the strong segregation limit, and demonstrate that the gyroid G phase is the most nearly stable among the bicontinuous phases considered. We explore some effects of conformational asymmetry on the topology of the phase diagram.
Analytic weak-segregation theory of bicontinuous phases in diblock copolymers S. T. Milner and P. D. Olmsted, Journal de Physique II 7 (1997) 249-255. (at Journal de Physique)
We compute phase diagrams for diblock copolymers in the mean-field weak-segregation regime as a function of the fraction f of A-monomers and the repulsive interaction \chi M. We include the ordered bicontinuous double-diamond (OBDD) phase [space group Pn3m] and the gyroid phase [space group Ia3d] as well as lamellae, hexagonal cylinders, and BCC spheres. We find a stable region of gyroid phase between cylinders and lamellae just above the mean-field critical point, in agreement with numerical mean-field calculations. The stability of gyroid depends on the presence of the next higher [220] reflections in addition to the [211] fundamental. The gyroid free energy is favored by terms of the form \psi^3[211]\psi[220] and \psi^2[211]\psi[220]; the analogous terms are not permitted for OBDD.
Fluctuation Corrections to Mean-Field Theory for Homopolymer-Copolymer Macrophase Separation: Sequence Distribution Effects P. D. Olmsted and S. T. Milner, Macromolecules 27 (1994) 1964-1967.
Mean-field theories (Flory-Huggins, RPA) predict that the critical repulsive interaction parameter \chi_c for polymer-polymer phase separation is independent of the monomer sequence distribution. In this work we generalize the RPA to account for sequence distribution effects on the spinodal by including both composition and chemical potential fluctuations. We calculate \chi_c(p) for a blend of homopolymers and multiblock copolymers with 2p blocks, and find an architecture-dependent shift of relative order N^{-1/2}. This shift either increases or decreases as p is increased (corresponding to a more evenly distributed copolymer), depending roughly on whether the homopolymer is shorter or longer than the copolymer. Fluctuations also shift the critical composition away from the Flory-Huggins value, even in asymmetric homopolymer/homopolymer blends.
Strong-Segregation Theory of Bicontinuous Phases in Block Copolymers P. D. Olmsted and S. T. Milner, Physical Review Letters 72 (1994) 936-939; 74 (1995) 829.
We compute phase diagrams for diblock copolymers in the strong-segregation regime as a function of volume fraction \phi. We include the ordered bicontinuous double-diamond (OBDD) phase, which is found to be stable between cylinders and lamellae, consistent with experiment, for \phi (or 1-\phi) between 0.19 and 0.27. Our phase diagram relies on taking into account the hexagonal shape of the unit cell for the cylindrical phase, and the unique geometry of the OBDD phase.
|
Back to the
Olmsted Homestead |
Research Page | peter.olmsted.(at).georgetown.edu |