Flow-Induced Phase Transitions
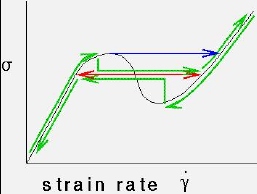The
internal
structure of complex fluids, such as liquid crystals, surfactant solutions,
or polymers, is rearranged and altered in flow. This shows up in measurements
of the stress as a function of strain rate, which is a boring straight
line for a simple fluid. In strong enough flows transitions can be induced
between phases, which gives rise to a non-monatonic stress-strain relation,
as shown here. The important question to understand is how the system `knows'
when to jump from the low to high shear branches.
Does it pick the red branch all the time
(which looks suspiciously like the Maxwell construction), does it jump
at the limit of stability, or does it take
a hysteretic path, depending on how fast the
system parameters are changed? Experiments seem to indicate that it takes
the hysteretic path, and steady states fall
on a plateau. It is tempting to treat such
transitions in the language of equilibrium phase transitions, which can
be fruitful as well as dangerous.
The curve shown here is just one of many topologically possible curves.
The isotropic-nematic transition in liquid crystalline systems has curves
which are multi-valued in both stress and strain rate, and experiments
have indicated the existence of systems which have a transition at either
a specified strain rate, or at a specified stress.
But wait, there's more. This is just one example. Fluids can also phase
separate into shear-thickening phases. There's a whole zoo out there waiting
to be tamed (or fed).
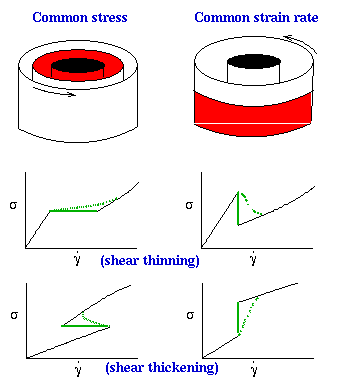The
figure on the right demonstrates the different possibilities for flow-induced
phase transitions. Either the two phases can have the same shear stress,
as on the left; or the two phases can have the same strain rate (specified
by the counter-rotating cylinders) as on the right. In the common stress
case (left) the strain rate varies in the two phases, while in the common
strain rate case (right) the shear stress is different in the two
phases. Hence the analog of
field and density variables in
equilibrum, such as pressure and density respectively, depends on the geometry
of the phase separation. The two lower rows show the possible rheological
signatures for shear-thinning (middle row) and shear-thickening (top row)
transitions, for the two geometries. The flat or vertical solid green lines
show the composite rheological signature if the
concentrations of
the coexisting phases are the same; while the curved dotted green lines
show what can happen if the concentrations in the coexisting phases differ.
The deviation from vertical (common strain rate) or horizontal (common
stress) depends on the details of the non-equilibrium phase diagram.