Coma

What is coma?

Coma is an aberration resulting from a variance in magnification depending on the ray height at the lens.

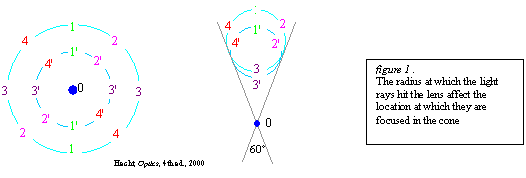
There are two types of coma: positive and negative. Negative coma occurs when rays hitting the lens further from the paraxial region focus closer to the axis than rays closer to the paraxial region. Positive coma is just the opposite, with the further rays focusing farther from the axis (figure 1).

What causes coma?

Coma result from the use of principle planes when considering the propagation of image through a system. The principle planes are only really planes in the paraxial region. As you move further from the paraxial region, the surface the rays strike is curved, affecting the focal length for these rays impacting where they focus on the object plane. The focusing of a ray is therefore dependent on the height off the axis at which it strikes the lens.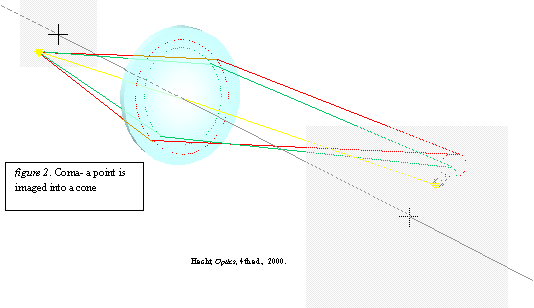

Why does it look like it does?

As rays strike the lens further from the center, each ray at a specific radius from the center in a plane will focus at a certain spot on the image plane. All of the rays striking at a particular radius on the lens create an off centered circle of the image plane, with the circle of the imge plane getting larger as the rays strike the lens further from the axis. This causes an object point to form a cone (figure 2).

Coma is easily seen by holding a lens in sunlight and then tilting it, creating an image that tails off to one side (figure 3).

How do we alter a system so there is no coma?

The optical sine theorem (Abbe sine condition) states that

(n_o) (y_o) (sin α_o) = (n_i) (y_i) (sin α_i)

where n_o, y_o, α_o and are the index of refraction, height, and slope angle of a ray in object space and n_i, y_i, α_i are the index of refraction, height, and slope angle of the ray in image space.

Since coma results from a change in magnification with height, for there to be no coma, the magnification must be constant everywhere:

Using the sine theorem, this means that .

Physically, this means the ratio of the angle at which the ray enters the lens to the angle at which the ray leaves the lens should be constant across the lens to avoid coma.

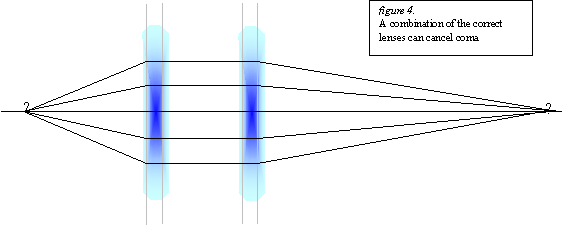
This ratio can be assured if the rays entering a lens originate at infinity (they are parallel). This can be done using a combination of lenses (figure 4).

A stop can also be placed in the system. The position of the stop affects the light rays getting through. A positive or negative coma can be created by selective positioning. This coma created by the stop can be used to cancel out coma present in the system independent of the stop.

References:

Born, Max & Wolf, Emil, Principles of Optics, 6^th Edition, Oxford: Pergamon Press, 1980.

Hecht, Eugene, Optics, 4^th Edition, San Francisco: Addison-Wesley, 2002.