Spherical
Aberration
Mathematically, the spherical aberration is described by the term with dependence on r4. This means that the focal length has a dependence on the distance from the optical axis where the ray hits the lens (figures 1 and 2).
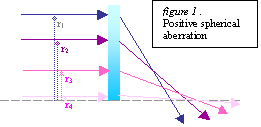
 A spherical aberration is considered
positive (figure 1) if the marginal rays focus closer to the lens than the
paraxial rays (a convex lens) or negative (figure 2) if the marginal rays focus
further from the lens than the paraxial rays.
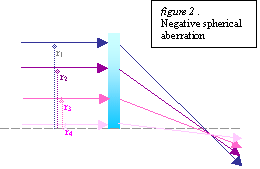
A spherical aberration is considered
positive (figure 1) if the marginal rays focus closer to the lens than the
paraxial rays (a convex lens) or negative (figure 2) if the marginal rays focus
further from the lens than the paraxial rays.
The distance along the optical axis over which the image is focused is called the longitudinal spherical aberration (figure 3).
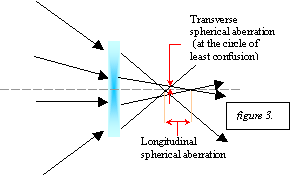 If a screen is placed at the
paraxial focus (the location at which the paraxial rays focus), the image will
be spread above and below the optical axis.
The distance from the outer most ray ot the optical axis is called the
transverse spherical aberration (figure 3).
There exists a point at which the transverse spherical aberration is the
least, and this is called the circle of least confusion.
If a screen is placed at the
paraxial focus (the location at which the paraxial rays focus), the image will
be spread above and below the optical axis.
The distance from the outer most ray ot the optical axis is called the
transverse spherical aberration (figure 3).
There exists a point at which the transverse spherical aberration is the
least, and this is called the circle of least confusion.
How does a spherical aberration affect the
image?
Spherical aberration creates a spreading of the light. This causes the image to appear fuzzy, lacking sharpness and definition.
How can we counteract spherical aberration?
The image can be improved by placing an aperture in the system to block the marginal rays. However, placing an aperture in the system will cut out these rays, causing the image to be dimmer.
Spherical aberration occurs because marginal rays are deviated more than the paraxial rays. Therefore, if we can reduce the deviation, we decrease the aberration. If we look at deviation through a prism we see that minimum deviation occurs when the marginal rays hit the first surface at approximately the same angle at which they hit the second surface. This same principle can be used with the lens: the image will undergo the least aberration if the marginal rays hit the first surface at the same angle which they strike the second surface.
The final option for eliminating spherical aberration for a single lens is to aspherize the lens – the lens is hand-polished to cause various areas of the lens surfaces to have different curvatures.
Hecht, Eugene, Optics, 4th Edition, San Francisco: Addison-Wesley, 2002.
Jenkins, Francis A. and Harvey E. White, Fundamentals of Optics, 4th Edition, New York: McGraw-Hill, 1976.