FOURIER PROPERTIES OF LENSES
In a sense, the lens is the simplest of optical computers because it instantly performs 2-dimensional Fourier transforms [2]. A Fourier transform is defined by
![]()
Let’s say that a plane-wave source of light illuminates
an aperture A, and that light emanates from the aperture into our
optical system. According to the Huygens-Fresnel principle, each
point within the aperture will act as a point source of light [2].
Following Hecht’s derivation, we assume that the source
strength ![]() is constant
over the aperture and that our source is coherent, yielding the
following equation:
is constant
over the aperture and that our source is coherent, yielding the
following equation:
![]()
Pick a point P on a screen a distance away from the aperture such that Frauenhofer diffraction will occur. If x is along the optical axis,
![]()
Substituting ![]() ,
and assuming (X,Y,Z) is the coordinate of point P:
,
and assuming (X,Y,Z) is the coordinate of point P:
![]()
![]()
In the Frauenhofer limit, the distance from the point to the aperture ~(X,Y,Z) is much larger than the dimensions of the aperture ~(x,y,z).
![]()
Thus, the electric field at a point P on our screen will be characterized by
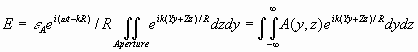
where ![]() is
defined as the aperture function. The new limits of plus and
minus infinity can be used because the aperture function is zero
for regions outside the aperture. If one defines the spatial
frequencies as
is
defined as the aperture function. The new limits of plus and
minus infinity can be used because the aperture function is zero
for regions outside the aperture. If one defines the spatial
frequencies as ![]() and
and ![]() , then we see it is
indeed the Fourier transform of our aperture function:
, then we see it is
indeed the Fourier transform of our aperture function:
![]()
In Frauenhofer diffraction, the screen should be at infinity for a perfect Fourier transform. The lens serves to bring this infinite focus to a desired length. Thus, a lens calculates the 2-D Fourier transform of our aperture source.
Special properties of Fourier transforms:
The correlation of two Fourier transforms is defined as:
![]() [6]
[6]
If f1 = f2, then we will have an autocorrelation function, which by the Wiener-Khintchine theorem is just the amplitude-squared of the fourier transform:
![]()
The convolution of two Fourier transforms is
![]()
With these two definitions in mind, we look at what a typical sinusoidal grating can do to an input signal. The transmittance function for the spatial filter in the frequency domain is
![]()
Where the exponential term is the plane wave reference, b is the separation between the reference and the corresponding point on the filter, and h refers to the filtering function itself. Now we are ready to send in our input signal f. With the help of our Fourier transform, the output signal will be:
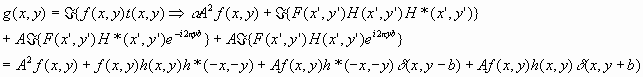
By the definitions outlined above, the third term is the correlation of f and h at (0,b). The fourth term is then the convolution of f and h at (0,-b). The first two terms are centered at the origin, and our terms of interest, the convolution and correlation, are located below and above the origin respectively. These will be of key interest in our optical filtering process, for they detail the degree to which the filter function and our input signal match.