DETAILS
Incoherent v. coherent
Optical computing using a coherent source is clearly the
simplest to compute and understand, but it has many practical
drawbacks. If one uses a transparency to create an input pattern,
our coherency is affected by changes in thickness in the film.
Also, any imperfections or dust on the optical components will
create an unwanted interference pattern due to scattering effects.
Incoherent processing, on the other hand, takes into account only
intensity, not phase, so just about anything, from a television
to a piece of paper can act as the input source. Also,
imperfections in the system have little effect on incoherent
light due to its redundant, multichannel nature [6]. On the other
hand, incoherent computing can never record phase information,
unlike coherent optical computing.
Filter fabrication
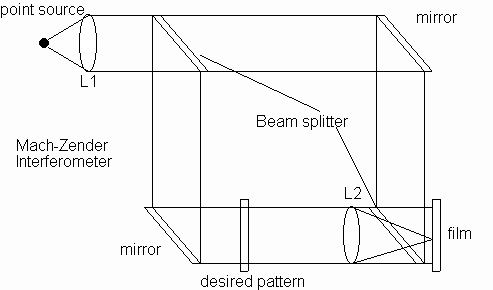 For coherent
processing, both amplitude and phase information can be stored on
a film, similar to the theory behind a hologram. The Mach-Zender
interferometer can be used to overlay a reference signal and our
desired impulse response onto a film which stores both phase and
the amplitude.
For coherent
processing, both amplitude and phase information can be stored on
a film, similar to the theory behind a hologram. The Mach-Zender
interferometer can be used to overlay a reference signal and our
desired impulse response onto a film which stores both phase and
the amplitude.
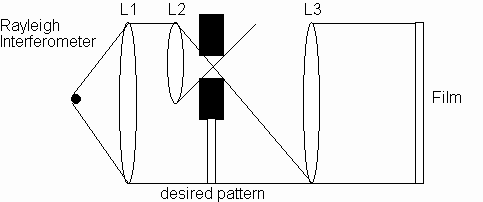 With the
Rayleigh Interferometer, the reference signal is focused through
the aperture one focal length in front of lens L3. This is then
collimated by lens L3, and thus overlayed with the desired
impulse response onto the film. One expense of this setup is the
elimination of spatial frequencies of the reference signal [4].
With the
Rayleigh Interferometer, the reference signal is focused through
the aperture one focal length in front of lens L3. This is then
collimated by lens L3, and thus overlayed with the desired
impulse response onto the film. One expense of this setup is the
elimination of spatial frequencies of the reference signal [4].
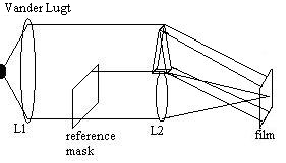 A better way
of performing this filtering process is through the Vander Lugt
filter [1]. This setup produces the crosscorrelation of the input
(f) with our reference filter (h) at the output [1]. To do so, we
must take our collimated light source and have a portion of it
strike the reference mask, while the rest of it is directed to
our photoresist film (see Figure 3). The light that passes
through the reference mask is Fourier transformed by a lens L2
and focused onto the same film [1]. This reference light will
only appear when the spectral lines of the input and the
reference match. The output plane will display the source at the
center, but as outlined in Goodman, the convolution and
crosscorrelation of the input and reference will appear off-axis
[1].
A better way
of performing this filtering process is through the Vander Lugt
filter [1]. This setup produces the crosscorrelation of the input
(f) with our reference filter (h) at the output [1]. To do so, we
must take our collimated light source and have a portion of it
strike the reference mask, while the rest of it is directed to
our photoresist film (see Figure 3). The light that passes
through the reference mask is Fourier transformed by a lens L2
and focused onto the same film [1]. This reference light will
only appear when the spectral lines of the input and the
reference match. The output plane will display the source at the
center, but as outlined in Goodman, the convolution and
crosscorrelation of the input and reference will appear off-axis
[1].
Filter fabrication for simple incoherent processing can be
made by either a film or a simple transparency. By placing a CCD
camera at the Fourier transform plane of our system with the
desired pattern as the source, the Fourier transform can easily
be captured and printed onto a transparency with a laser printer.
 For coherent
processing, both amplitude and phase information can be stored on
a film, similar to the theory behind a hologram. The Mach-Zender
interferometer can be used to overlay a reference signal and our
desired impulse response onto a film which stores both phase and
the amplitude.
For coherent
processing, both amplitude and phase information can be stored on
a film, similar to the theory behind a hologram. The Mach-Zender
interferometer can be used to overlay a reference signal and our
desired impulse response onto a film which stores both phase and
the amplitude.  With the
Rayleigh Interferometer, the reference signal is focused through
the aperture one focal length in front of lens L3. This is then
collimated by lens L3, and thus overlayed with the desired
impulse response onto the film. One expense of this setup is the
elimination of spatial frequencies of the reference signal [4].
With the
Rayleigh Interferometer, the reference signal is focused through
the aperture one focal length in front of lens L3. This is then
collimated by lens L3, and thus overlayed with the desired
impulse response onto the film. One expense of this setup is the
elimination of spatial frequencies of the reference signal [4]. A better way
of performing this filtering process is through the Vander Lugt
filter [1]. This setup produces the crosscorrelation of the input
(f) with our reference filter (h) at the output [1]. To do so, we
must take our collimated light source and have a portion of it
strike the reference mask, while the rest of it is directed to
our photoresist film (see Figure 3). The light that passes
through the reference mask is Fourier transformed by a lens L2
and focused onto the same film [1]. This reference light will
only appear when the spectral lines of the input and the
reference match. The output plane will display the source at the
center, but as outlined in Goodman, the convolution and
crosscorrelation of the input and reference will appear off-axis
[1].
A better way
of performing this filtering process is through the Vander Lugt
filter [1]. This setup produces the crosscorrelation of the input
(f) with our reference filter (h) at the output [1]. To do so, we
must take our collimated light source and have a portion of it
strike the reference mask, while the rest of it is directed to
our photoresist film (see Figure 3). The light that passes
through the reference mask is Fourier transformed by a lens L2
and focused onto the same film [1]. This reference light will
only appear when the spectral lines of the input and the
reference match. The output plane will display the source at the
center, but as outlined in Goodman, the convolution and
crosscorrelation of the input and reference will appear off-axis
[1].