Annotated Publications for James K. Freericks

Review Articles

• J. K. Freericks and V. Zlatic', Exact dynamical mean field theory of the Falicov-Kimball model, Rev. Mod. Phys. 75, 1333--1382 (2003).
  A comprehensive review of equilibrium properties of the Falicov-Kimball model, solved with dynamical mean field theory. The formalism is developed from a path-integral approach.
• J. K. Freericks, B. K. Nikolic, and P. Miller, Optimizing the speed of a Josephson junction with dynamical mean-field theory, Int. J. Mod. Phys. B 16, 531--561 (2002).
  A review of the application of the local approximation and the Falicov-Kimball model to the theory of Josephson junctions with barriers tuned near the metal-insulator transition.
• V. Zlatic', J. K. Freericks, R. Lemanski, and G. Czycholl, Exact solution of the multi-component Falicov-Kimball model in infinite dimensions, Phil. Mag. B 81, 1443 (2001).
  A mini review of the Falicov-Kimball model that emphasizes an equation of motion approach. Properties of both conduction and localized electrons are included as well as a discussion of spontaneous hybridization.
• Th. Pruschke, M. Jarrell, and J. K. Freericks, Anomalous Normal-State Properties of High-Tc Superconductors -- Intrinsic Properties of Strongly Correlated Electron Systems?, Adv. Phys. 44 187--210 (1995).
  A short review of dynamical mean field theory for the Hubbard model with an emphasis on transport properties.
• J. K. Freericks and M. Jarrell, Simulation of the electron-phonon interaction in infinite dimensions, in Computer Simulations in Condensed Matter Physics VII, edited by D. P. Landau, K. K. Mon, and H.-B. Schuttler (Springer-Verlag, Heidelberg, Berlin, 1994).
  A short review of the numerical techniques for performing quantum Monte carlo simulations of the electron-phonon problem in infinite dimensions.

Josephson Junctions

• B. K. Nikolic, J. K. Freericks, and P. Miller, Reduction of Josephson critical current in short ballistic SNS weak links, Phys. Rev. B 64, 212507--1-4 (2001).
  B. K. Nikolic, J. K. Freericks, and P. Miller, Suppression of the ``quasiclassical'' proximity gap in correlated-metal--superconductor structures, Phys. Rev. Lett. 88, 077002-1--4 (2002); Virtual Journal of Nanoscale Science & Technology, Vol. 5, Iss. 7.
  B. K. Nikolic, J. K. Freericks, and P. Miller, Equilibrium properties of double-screened-dipole-barrier SINIS Josephson junctions, Phys. Rev. B 65, 064529-1--11 (2002); Virtual Journal of Applications of Superconductivity, Vol. 2, Iss. 3.
  P. Miller and J. K. Freericks, Microscopic self-consistent theory of Josephson junctions including dynamical electron correlations, J. Phys.: Conden. Mat. 13 3187--3213 (2001)
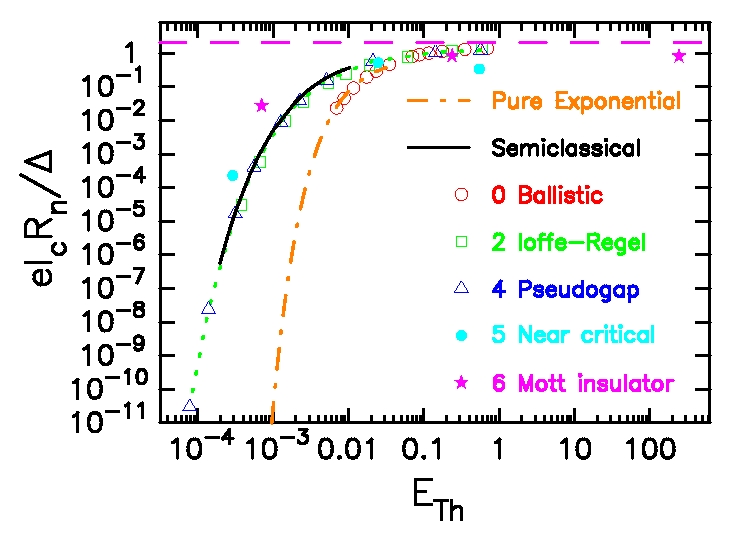
  In this series of papers, we generalize dynamical mean field theory to solve inhomogeneous systems in the superconducting phase. We discover a number of new results that arise from the self-consistent description of a Josephson junction including (i) the proposal that SNSNS structures with a narrow S layer within the normal metal barrier can have dramatically improved characteristic voltages; (ii) the suppresion of the quasiclassical minigap due to electron correlations; (iii) the reduction of characteristic voltage due to Schottky-like charge rearrangements at the superconductor-normal metal interface; and (iv) a reduction of the characteristic voltage due to the proximity and inverse proximity effects in ballistic junctions.



• J. K. Freericks, B. K. Nikolic, and P. Miller, Superconductor-Correlated Metal-Superconductor Josephson junctions: an optimized class for high speed digital electronics, (Proceedings of the Applied Superconductivity Conference, Houston, Texas) IEEE Trans. Appl. Supercond. 13, 1089 (2003).
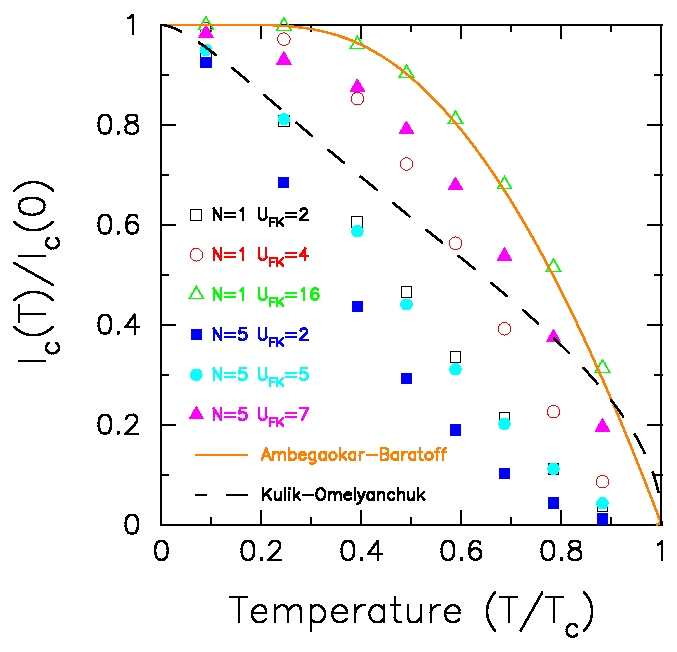
  J. K. Freericks, B. K. Nikolic, and P. Miller, Temperature dependence of Superconductor-Correlated Metal-Superconductor Josephson junctions, Appl. Phys. Lett. 82, 970--972 (2003); Virtual Journal of Applications of Superconductivity, 4, Issue 4 (2003); Erratum Appl. Phys. Lett. 83, 1275 (2003).
  J. K. Freericks, B. K. Nikolic, and P. Miller, Tuning a Josephson junction through a quantum critical point, Phys. Rev. B 64, 054511 (2001).
  In this series of papers, we concentrate on what happens to a Josephson junction as the barrier material is tuned from a metal to an insulator. We find a number of interesting resuts, including the possibility of having self-shunted junctions that have the fastest switching times.

Superconductivity in real materials

• J. K. Freericks, Amy Y. Liu, A. Quandt, and J. Geerk, Nonconstant electronic density of states tunneling inversion for A15 superconductors: Nb₃Sn, Phys. Rev. B 65, 224510--1-10 (2002).
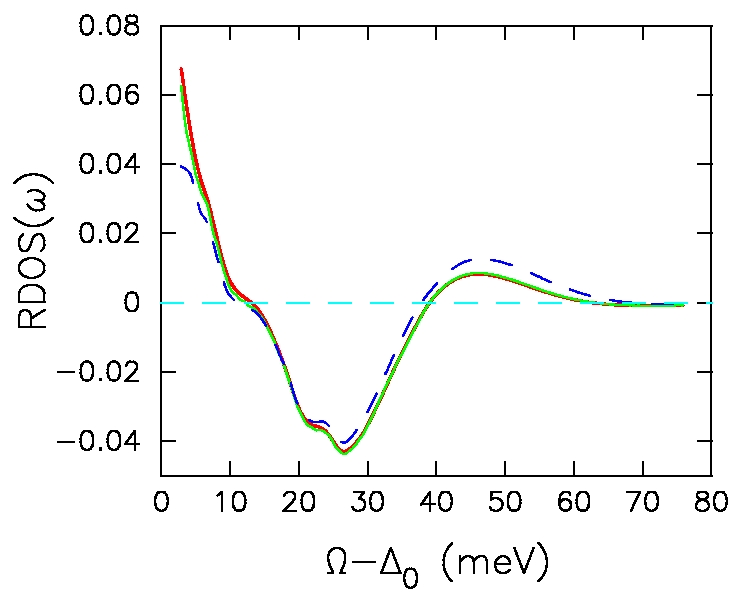
  We reexamine the tunneling data for A15 compounds using a tunneling formalism that incorporates the nonconstant electronic density of states that is calculated with density functional theory. The sharp peak in the DOS modifies the tunneling conductance, but it is not enough to fully explain the so-called "overswing".
• Sven P. Rudin, Amy Y. Liu, J. K. Freericks, and A. Quandt, Comparison of structural transformations and superconductivity in compressed Sulfur and Selenium, Phys. Rev. B 63, 224107 (2001).
  J. K. Freericks, S. P. Rudin, and A. Y. Liu, First-principles determination of superconducting properties of metals, Physica B 284-288, 425-426 (2000)
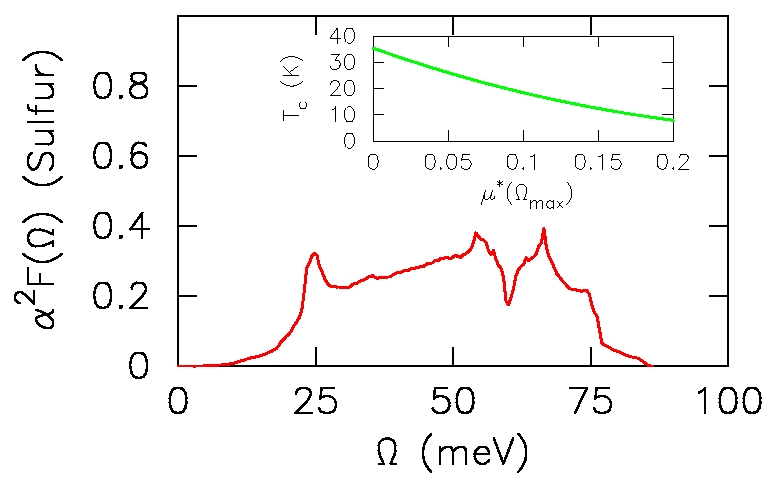
  This work plots out the phase diagram of chalcogenides under high pressure. Sulfur becomes the highest temperature elemental superconductor when it metallizes, but has large changes in Tc as the pressure tunes it through a series of structural transitions. Selenium and Tellurium behave in a similar fashion, but never are stabilized in a simple-cubic phase as Sulfur is.



• A. Y. Liu,, A. A. Quong, J. K. Freericks, E. J. Nicol, and E. C. Jones, Structural phase stability and electron-phonon coupling in Lithium, Phys. Rev. B 59, 4028--4035 (1999).
  This paper deals with a long-standing puzzle: why is it that Lithium and Aluminum have almost the same electron-phonon coupling but Aluminun superconducts at about 1K, while Lithium is not superconducting down to 0.004K? We show that the stable low-temperature phase of Lithium (which is determined by an ``honest'' quasiharmonic analysis) has a smaller electron-phonon coupling and conventional theory could explain a superconducting Tc down to about 0.001K beyond which other explanations would need to be found to resolve the puzzle. Experiments at Berkeley have not found any sign of superconductivity down to 0.005K, but they did see a large Curie-like magnetic response, so Lithium may have some more surprises for us.



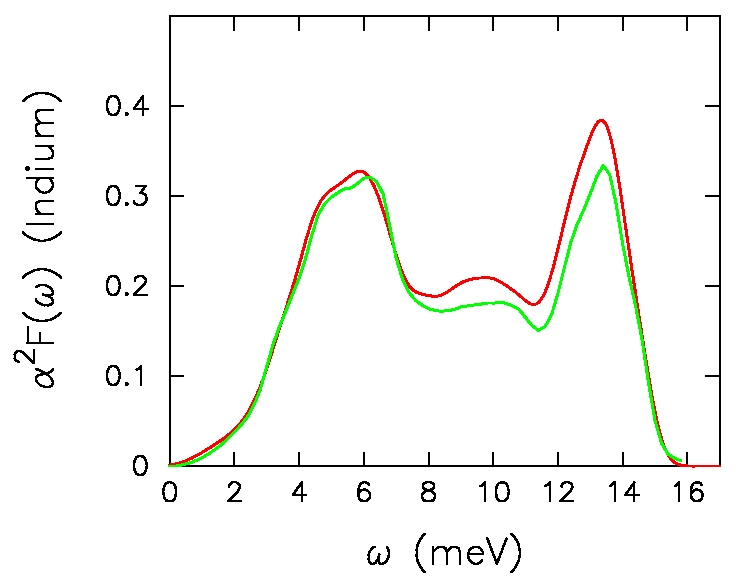
• S. P. Rudin, R. Bauer, A. Y. Liu, and J. K. Freericks, Reevaluating electron-phonon coupling strengths: Indium as a test case for ab initio and many-body-theory methods, Phys. Rev. B 58, 14511--14517 (1998).
  J. K. Freericks, E. J. Nicol, A. Y. Liu, and A. A. Quong, Vertex-corrected tunneling inversion in superconductors, Czechoslovak Journal of Physics 46, Supplement S2, 603-604 (1996).
  Here we examine how to calculate the tunneling density of states of Indium using only one adjustable parameter---the Coulomb pseudopotential. We find that our theoretical results are as accurate as an experimental fit to the data (better than one part in 10,000), which illustrates that current theoretical methods can rival those of experiment for low-temperature superconductors. In the process, we discovered that even though the data can be fit quite accurately, the value of the electron-phonon coupling may have errors as high as 20%.






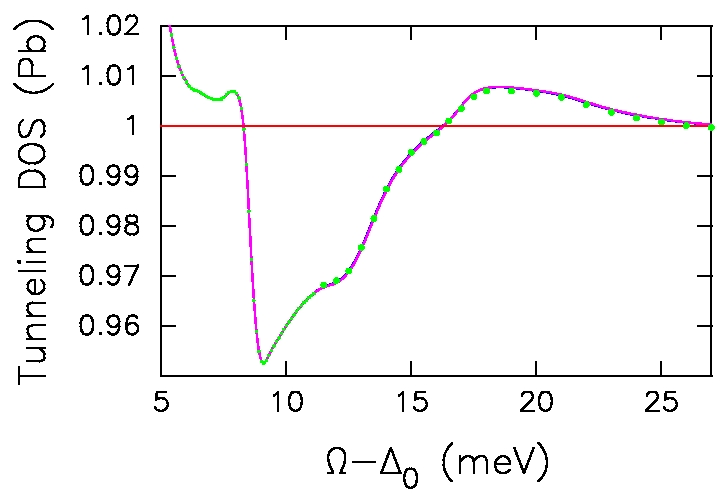
• J. K. Freericks, E. J. Nicol, A. Y. Liu, and A. A. Quong, Vertex-corrected tunneling inversion in electron-phonon mediated superconductors: Pb, Phys. Rev. B, 55, 11651--11658 (1997).
  We generalize the conventional Migdal-Eliashberg theory to include vertex corrections and see if effects of vertex corrections can be seen in Lead. We find that the effects of the vertex corrections are just on the edge of being able to be seen in Lead (the difficulty arises from the very low phonon frequencies in Lead, which suppress vertex correction effects). This technique can be employed on other materials like the fullerenes or cubic perovskites, whenever high quality tunneling data is produced for them.

Raman scattering, optical conductivity, and transport

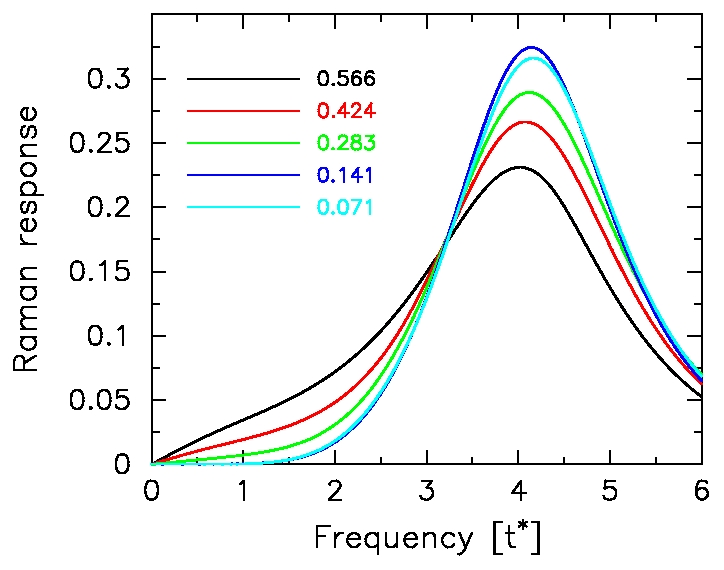
• J. K. Freericks, T. P. Devereaux, and R. Bulla, Inelastic light scattering and the correlated metal-insulator transition, (Proceedings of the NATO ARW on strongly correlated electrons, Hvar, Croatia) Nato Science series II: Mathematics Physics and Chemistry: Vol. 110 (Kluwer, Dordrecht, 2003), p. 115--122.
  J. K. Freericks, T. P. Devereaux, and R. Bulla, Inelastic Light Scattering and the Correlated metal-Insulator Transition, (Proceedings of the Strongly Correlated Electrons conference, Krakow, Poland) Acta Physica Polonica B 34, 737--748 (2003).
  J. K. Freericks, T. P. Devereaux, R. Bulla, and Th. Pruschke, Nonresonant inelastic light scattering in the Hubbard model, Phys. Rev. B 67, 155102--1-8 (2003).
  F. Venturini, M. Opel, T. P. Devereaux, J. K. Freericks, I. Tutto, B. Revaz, E. Walker, H. Berger, L. Forro, and R. Hackl, Observation of an unconventional metal-insulator transition in overdoped CuO₂ compounds, Phys. Rev. Lett. 89, 107003--1-4 (2002).
  J. K. Freericks, T. P. Devereaux, and R. Bulla, An exact theory for Raman scattering in correlated metals and insulators, Phys. Rev. B 64, 233114 (2001).
  J. K. Freericks and T. P. Devereaux, Raman scattering through a metal-insulator transition, Phys. Rev. B 64, 125110 (2001).
  
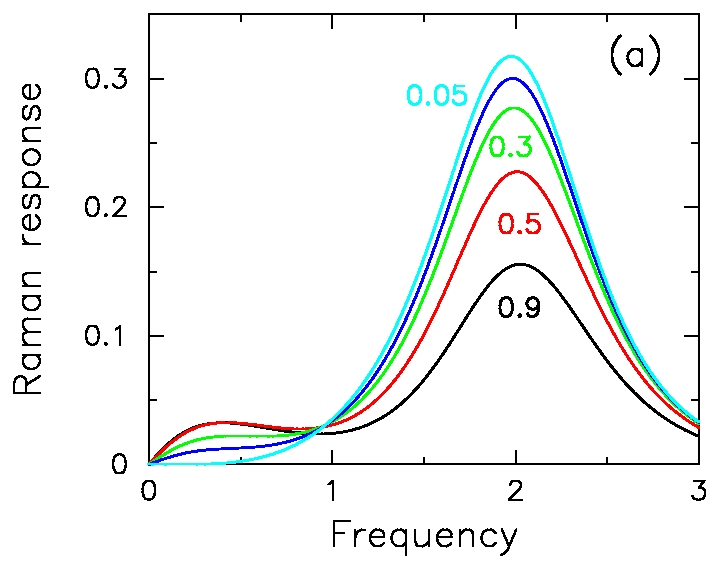J. K. Freericks, T. P. Devereaux, and R. Bulla, B1g Raman scattering through a quantum critical point, (Proceedings of the XIIth school of modern physics on phase transitions and critical phenomena, Ladek Zrdoj, Poland) Acta Physica Polonica B 32, 3219--3232 (2001).
J. K. Freericks and T. P. Devereaux, Non-resonant Raman scattering through a metal-insulator transition: an exact analysis of the Falicov-Kimball model, (Proceedings of the Workshop on Soft Matter Theory, Lviv, Ukraine) Conden. Matter Phys. (Ukraine) 4, 149--160 (2001).
This is the first work to calculate a Raman response for a system that undergoes a metal-insulator transition. We find that our results are universal on the insulating side of the metal-insulator transition and display the three fundamental features seen in experiment on strongly correlated materials: (i) a rapid loss of low-energy spectral weight and a gain of high-energy spectral weight as temperature is lowered; (ii) the appearance of an isosbestic point, where the Raman response is independent of temperature at a characteristic frequency; and (iii) the ratio of the range in frequency over which the Raman response is depleted at low temperature to the onset temperature where the depletion begins is large. This behavior has been seen SmB₆, FeSi, and the high-temperature superconductors. The extension of the nonresonant work to the resonant case represents one of the most complex solutions to a many-body problem with DMFT.
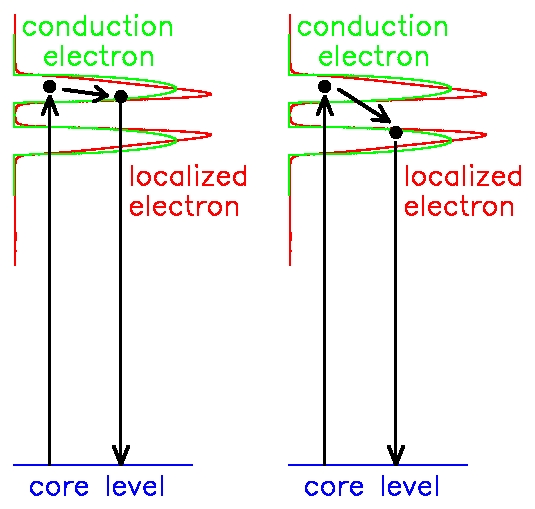• J. K. Freericks, T. P. Devereaux, R. Bulla, and Th. Pruschke, Nonresonant inelastic light scattering in the Hubbard model, Phys. Rev. B 68, 075105--1-11 (2003).
  T. P. Devereaux, G. E. D. McCormack and J. K. Freericks, Inelastic x-ray scattering in correlated (Mott) insulators, Phys. Rev. Lett. 90, 067402--1-4 (2003).
  In this work, we focus on the light scattering by X-rays which can exchange both momentum and energy with the electronic charge excitations of the correlated material. We see dispersion of some quantities, the appearance of isosbestic points throughout the Brillouin zone, and a way to test for the effects of nonlocal charge fluctuations by appropriately using polarizers. Further extensions will include a description of the resonant inelastic x-ray scattering process which is an interesting new experimental technique employed to examine charge excitations of correlated materials.





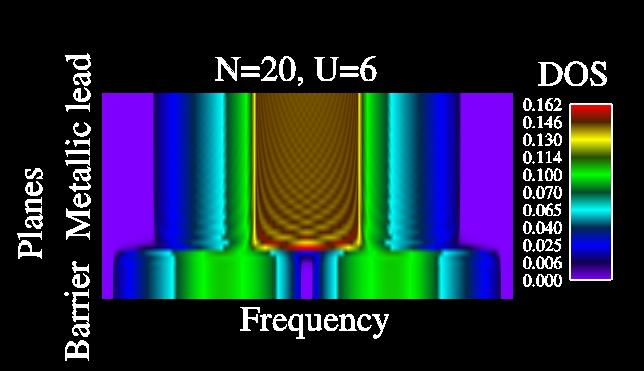• J. K. Freericks, Crossover from tunneling to incoherent (bulk) transport in a correlated nanostructure, Appl. Phys. Lett. 84, 1383--1385 (2004); Virtual Journal of Nanoscale Science and Technology, 9, Issue 8 (2004); Virtual Journal of Applications of Superconductivity, 6, Issue 5 (2004).
  In this work we examine how the transport in a multilayer nanostructure changes from tunneling (for thin barriers at low temperature) to incoherent Ohmic transport (for thick barriers at high temperature). We develop the theory of a generalized Thouless energy that describes the crossover.
• B. K. Nikolic and J. K. Freericks, Mesoscopics in spintronics: Quantum interference effects in spin-polarized electrons, submitted to Phys. Rev. B.
  B. K. Nikolic and J. K. Freericks, Mesoscopic spintronics: Fluctuation and localization effects in spin-polarized quantum transport, Toward the controllable quantum states, edited by H. Takayanagi and J. Nitta (World Scientific, 2003).
  Papers on spintronics and the Rashba coupling.
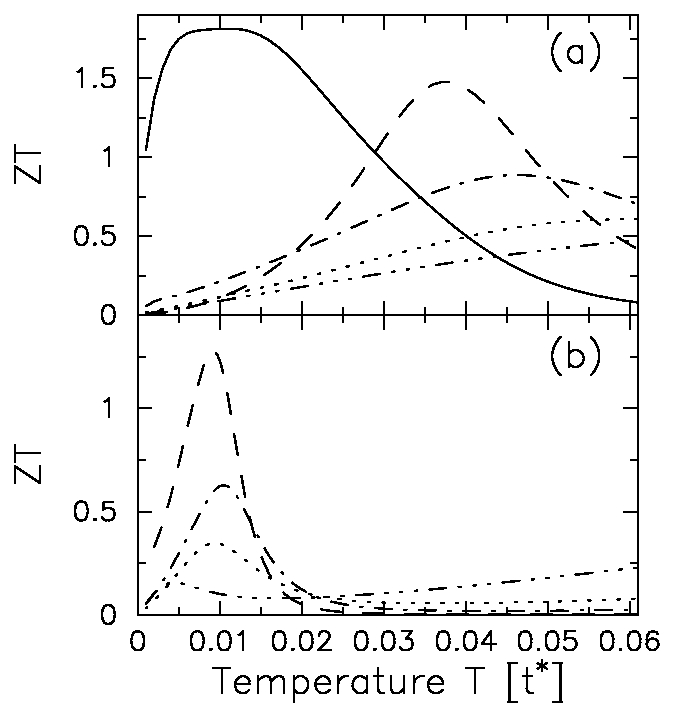• A. V. Joura, D. O. Demchencko, and J. K. Freericks, Thermal transport in the Falicov-Kimball model on a Bethe lattice, Phys. Rev. B 69, 165105--1-5 (2004).
  J. K. Freericks, D. Demchenko, A. Joura, and V. Zlatic', Optimizing thermal transport in the Falicov-Kimball model: binary-alloy picture, Phys. Rev. B 68, 195120--1-12 (2003).
  J. K. Freericks and V. Zlatic', Thermal transport in the Falicov-Kimball model, Phys. Rev. B 64, 245118--1-10 (2001); Erratum: Phys. Rev. B 66, 249901--1-2 (2002).
  Here we examine what happens to thermal transport properties in the Falicov-Kimball model. We are able to explicitly prove the Jonson-Mahan theorem and find regions where the thermoelectric figure of merit is larger than one both at low temperature and high temperature. But it is likely the low temperature peaks will disappear when phonon thermal conductivity is included. We also find quite different behavior on the hypercubic lattice versus the Bethe lattice which is due to anomalous features associated with the pseudogap nature of the insulating phase on the hypercubic lattice.
• B.M. Letfulov and J. K. Freericks, Dynamical mean-field theory of a double-exchange model with diagonal disorder, Phys. Rev. B 64, 174409 (2001).
  My only paper on the colossal magnetoresistance materials.




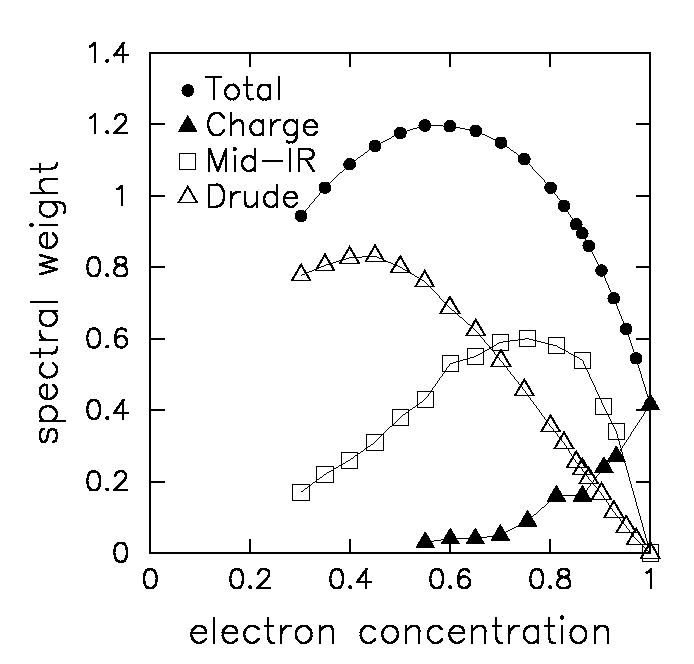• M. Jarrell, J. K. Freericks, and Th. Pruschke, Optical conductivity of the infinite-dimensional Hubbard model, Phys. Rev. B 51 , 11704-11711 (1995).
  Here we examine the appearance of midinfrared response in the optical conductivity for a correlated metal described by the Hubbard model. One of the interesting results we find is the appearance of an isosbestic point---where the optical conductivity is independent of electron concentration at a characteristic frequency.
• J. K. Freericks and L. M. Falicov, Dephasing effects in a two-dimensional magnetic-breakdown linked-orbit network: Magnesium, Phys. Rev. B 39, 5678-5683 (1989).
  My first paper in condensed matter physics, this work examined how disorder, induced by thermal quenching of ultrapure samples of Magnesium, modifies the transport of electrons in the presence of a perpendicular magnetic field. This simple model produced remarkable agreement with the experimental data that was measured in the sixties.

Models of Strong Electron Correlations

Falicov-Kimball Model

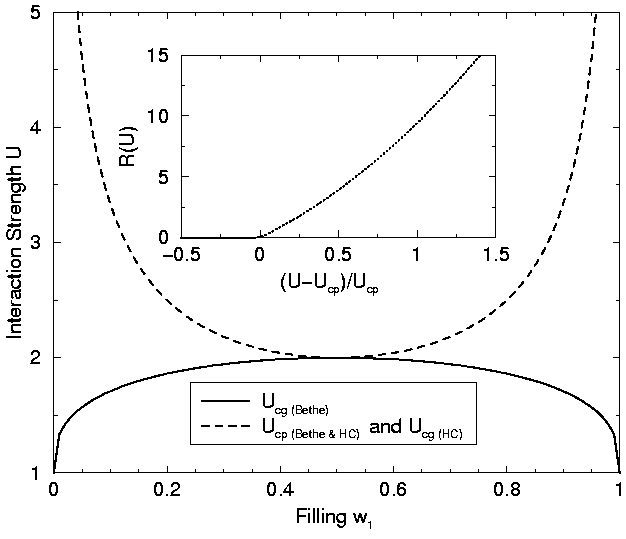• D. O. Demchencko, A. V. Joura, and J. K. Freericks, Effect of particle-hole asymmetry on the Mott-Hubbard metal-insulator transition Phys. Rev. Lett. 92, 216401--1-4 (2004).
  This work shows that the metal-insulator transition in dynamical mean field theory is not always governed by the creation of a pole in the self energy at the transition.l On systems with a finite bandwidth, the MIT usually occurs before a pole forms, and the model does not have any significant change in its properties when a pole subsequenctly forms at a larger interaction strength.
• A. M. Shvaika and J. K. Freericks, Equivalence of the Falicov-Kimball and Brandt-Mielsch forms for the free energy of the infinite-dimensional Falicov-Kimball model, Phys. Rev. B 67, 153103--1-3 (2003).
  
• This work is almost a textbook derivation of the equivalence of two apparently different ways to calculate the free energy of the Falicov-Kimball model.
• R. Lemanski, J.K. Freericks and G. Banach, Stripe phases in the two-dimensional Falicov-Kimball model, Phys. Rev. Lett. 89 196403-1--4 (2002).
  Here we show how stripe-like phases naturally arise in the two-dimensional Falicov-Kimball model as the system changes from a checkerboard pattern at half filling to a segregated system at low filling.
• J. K. Freericks, E. H. Lieb, and D. Ueltschi, Phase separation due to quantum mechanical correlations, Phys. Rev. Lett. 88, 106401--1-4 (2002).
  J. K. Freericks, E. H. Lieb, and D. Ueltschi, Segregation in the Falicov-Kimball model, Commun. Math. Phys. 227, 243--279 (2002).
  In this work, we solved a long-standing problem that proved that the Falicov-Kimball model always phase separates when the interaction strength is large enough on any lattice in any dimension.
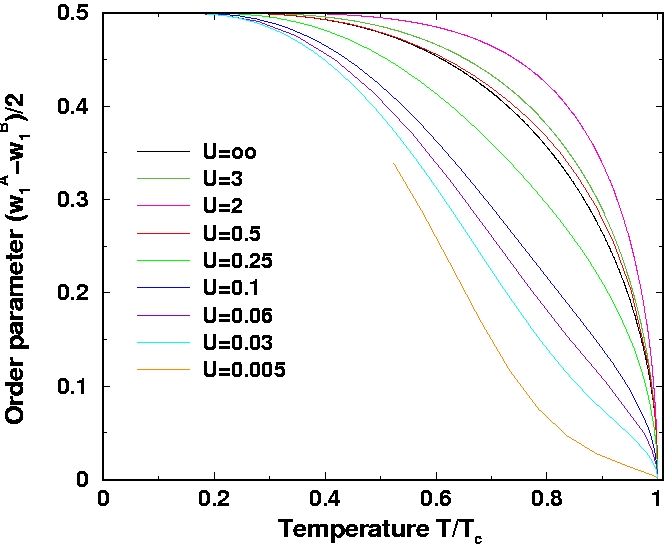
• Ling Chen, B. A. Jones, and J. K. Freericks, Charge-density-wave order parameter of the Falicov-Kimball model in infinite dimensions, Phys. Rev. B 68, 153102--1-4 (2003).
  Ch. Gruber, N. Macris, Ph. Royer, and J. K. Freericks, Higher period ordered phases on the Bethe lattice, Phys. Rev. B. 63, 165111-1--11 (2001).
  We examine the charge-density wave ordered phase of the Falicov-Kimball model. In the 2003 paper, we examine the order parameter as a function of temperature, and see that it has an anomalous shape for weak coupling. In the 2001 paper, we explicitly show how to generate a period-three phase on an infinite-coordination Bethe lattice. Surprisingly, these phases are stable only at very low temperature, and typically have first-order phase transitions.



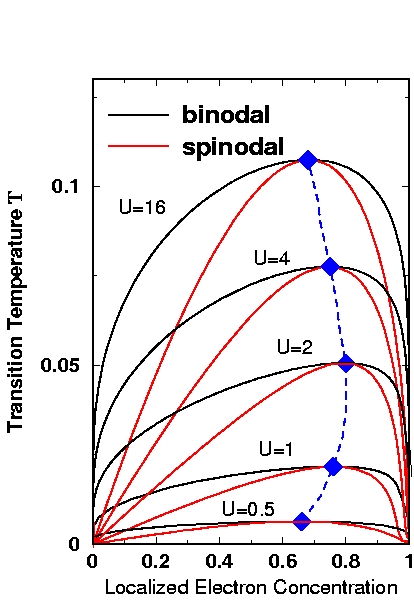
• J. K. Freericks and P. Miller, Dynamical charge susceptibility of the spinless Falicov-Kimball model, Phys. Rev. B 62, 10022--10032 (2000).
  We use Kadanoff-Baym theory to derive the frequency dependent charge susceptibility for the Falicov-Kimball model, which is one of the few many-body systems that one can exactly solve for a dynamical susceptibility. These results were used heavily in deriving Raman scattering behavior for nontrivial symmetry sectors.
• B.M. Letfulov and J. K. Freericks, Phase separation in the combined Falicov-Kimball and static Holstein model, Phys. Rev. B 66, 033102-1--4 (2002).
  J. K. Freericks and R. Lemanski, Segregation and charge-density-wave order in the spinless Falicov-Kimball model, Phys. Rev. B 61 13438--13444 (2000).
  J. K. Freericks, Ch. Gruber, and N. Macris, Phase separation and the segregation principle in the infinite-U spinless Falicov-Kimball model, Phys. Rev. B 60 1617--1626 (1999).
  J. K. Freericks, Ch. Gruber, and N. Macris, Phase separation in the binary-alloy problem: the one-dimensional spinless Falicov-Kimball model, Phys. Rev. B 53, 16189-16196 (1996).
  J. K. Freericks, Local approximation to the spinless Falicov-Kimball model, Phys. Rev. B 48, 14797-14801 (1993).
  J. K. Freericks, Spinless Falicov-Kimball model (annealed binary alloy) from large to small dimensions, Phys. Rev. B 47, 9263-9272 (1993).
  J. K. Freericks and L. M. Falicov, Two-state one-dimensional spinless Fermi gas, Phys. Rev. B 41, 2163-2172 (1990).
  These series of papers examine phase separation and charge-density-wave order in the Falicov-Kimball model. Results range from numerical calculations on one-dimensional or infinite-dimensional systems, to rigorous results for small or large coupling strength. One of the interesting results coming from this work is the strong tendency for electron repulsion to favor phase separation, which has been seen in the charge-stripe phase of the cuprate materials.



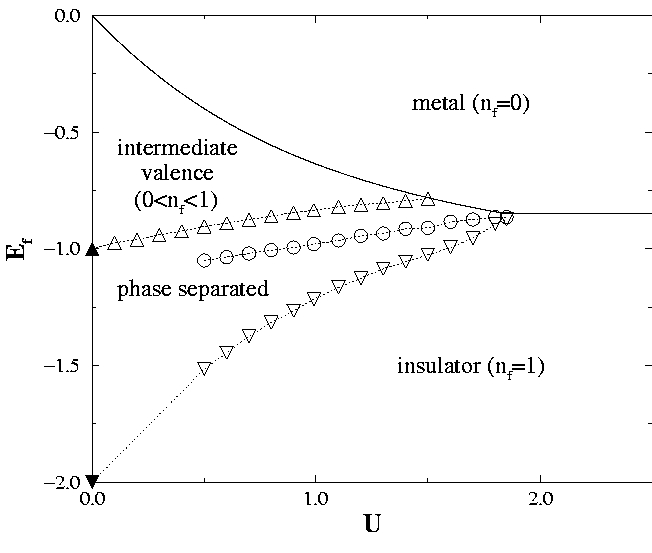
• Woonki Chung and J. K. Freericks, Competition between phase separation and ``classical'' intermediate valence in an exactly solved model, Phys. Rev. Lett. 84, 2461--2464 (2000).
  Woonki Chung and J. K. Freericks, Charge-transfer metal-insulator transitions in the spin-one-half Falicov-Kimball model, Phys. Rev. B 57 11955--11961 (1998).
  J. K. Freericks and L. M. Falicov, Thermodynamic model of the insulator-metal transition in nickel iodide, Phys. Rev. B 45, 1896-1899 (1992).
  These publications examine metal-insulator transitions and intermediate-valence behavior, providing an exact solution that proves first-order transitions exist in the Falicov-Kimball model. In addition, we found that phase separation or a direct metal-insulator transition usually preclude intermediate-valence behavior over a wide range of parameter space.




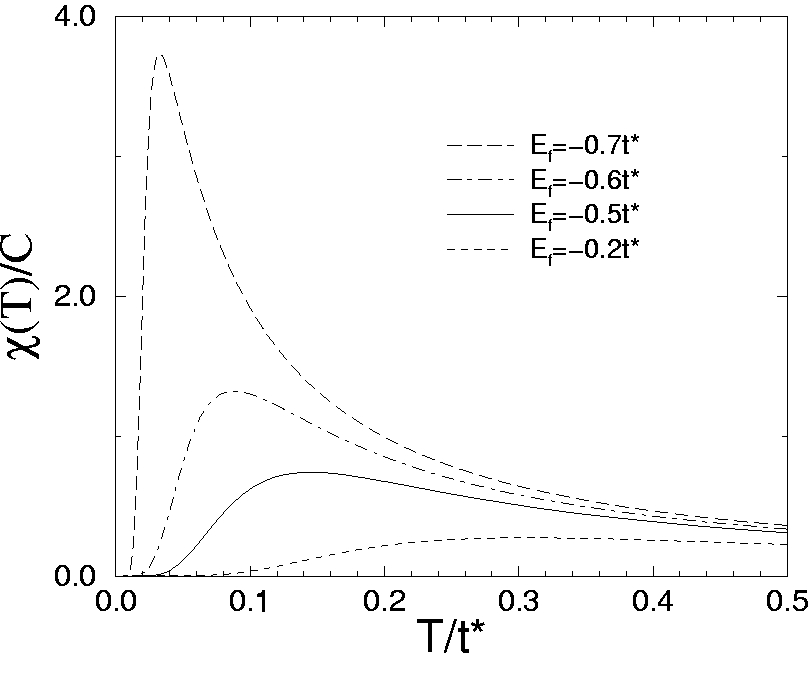• V. Zlatic' and J. K. Freericks, Describing the valence-change transition by the DMFT solution of the Falicov-Kimball model, (Proceedings of the NATO ARW on strongly correlated electrons, Hvar, Croatia) to be published (Kluwer).
  V. Zlatic' and J. K. Freericks, DMFT solution of the Falicov-Kimball model with an internal structure, (Proceedings of the Strongly Correlated Electrons conference, Krakow, Poland) Acta Physica Polonica B 34, 931--944 (2003).
  J. K. Freericks and V. Zlatic', Application of the multicomponent Falicov-Kimball model to intermediate-valence materials: YbInCu₄ and EuNi₂(Si_1-xGe_x)₂, (Proceedings of the Physics of Magnetism, Poznan, Poland), physica status solidi (b) 236, 265--271 (2003).
  V. Zlatic' and J. K. Freericks, Theory of valence transitions in Ytterbium and Europium intermetallics, (Proceedings of the XIIth school of modern physics on phase transitions and critical phenomena, Ladek Zrdoj, Poland) Acta Physica Polonica B 32, 3253--3266 (2001).
  V. Zlatic' and J. K. Freericks, Theory of valence transitions in ytterbium-based compounds, in Open Problems in Strongly Correlated Electron Systems, edited by J. Bonca, P. Prelovsek, A. Ramsak, and S. Sarkar, (Kluwer, Dordrecht, 2001) p. 371--380 [NATO Science Series, II. Mathematics, Physics, and Chemistry--Vol. 15] (Proceedings of NATO ARW conference, Bled, Slovenia, 2001).
  J. K. Freericks and V. Zlatic', Anomalous magnetic response of the spin-one-half Falicov-Kimball model, Phys. Rev. B 58 322--329 (1998).
  Here we examine the anomalous properties of the YbInCu4 system. We find that this material, which undergoes a finite temperature intermediate valence phase transition, is described well by the Falicov-Kimball model at high temperatures, where a metal-insulator transition drives the electronic density of states down, so hybridization effects are not very important. As the temperature is lowered, the system is described better by a periodic Anderson model. Our initial interpretation of the data, in terms of ill-placed and properly placed Yb atoms, turned out not to be borne out by experiment.

Hubbard Model

• A. N. Tahvildar-Zadeh, J. K. Freericks, and M. Jarrell, Magnetic phase diagram of the Hubbard model in three dimensions: the second-order local approximation, Phys. Rev. B 55, 942-946 (1997).
  This is a cute paper that uses a very simple modification of the Stoner criterion to include the lowest-order effect of quantum fluctuations in calculating the magnetic phase diagram of the Hubbard model. We found remarkable agreement with the shape of the phase diagram of Chromium alloys. Much better than one would ever expect to be able to produce from such a simple model.
• J. K. Freericks and M. Jarrell, Magnetic phase diagram of the Hubbard model, Phys. Rev. Lett. 74 , 186-189 (1995).
  Here we calculate the phase diagram of the Hubbard model using quantum Monte Carlo simulation. One of the interesting results is the presence of incommensurate magnetic order, and another is the lack of any ferromagnetic phases.

Periodic Anderson Model

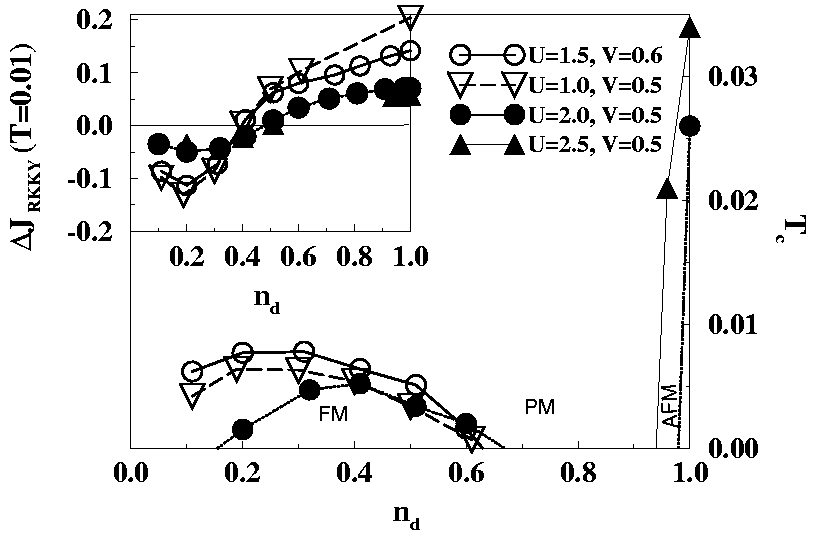
• A. N. Tahvildar-Zadeh, M. Jarrell, Th. Pruschke, and J. K. Freericks, Evidence for exhaustion in the conductivity of the infinite-dimensional periodic Anderson model, Phys. Rev. B 60, 10782--10787 (1999).
  A. N. Tahvildar-Zadeh, M. Jarrell, and J. K. Freericks, Low-temperature coherence in the periodic Anderson model: Predictions for photoemission of heavy Fermions, Phys. Rev. Lett. 80 5168--5171 (1998).
  A. N. Tahvildar-Zadeh, M. Jarrell, and J. K. Freericks, Protracted screening in the periodic Anderson model, Phys. Rev. B 55, 3332-3335 (1997) (Rapid Communication)
  This series of papers covers phenomena related to exhaustion physics in the periodic Anderson model. This occurs when there are fewer conduction electrons than f-electrons to be able to screen all of the local moments except as a collective process. As a result, there are interesting predictions about what should be seen in photoemission and optical conductivity measurements, which agree with that observed for some heavy-fermion or intermediate-valence materials.

Holstein Model

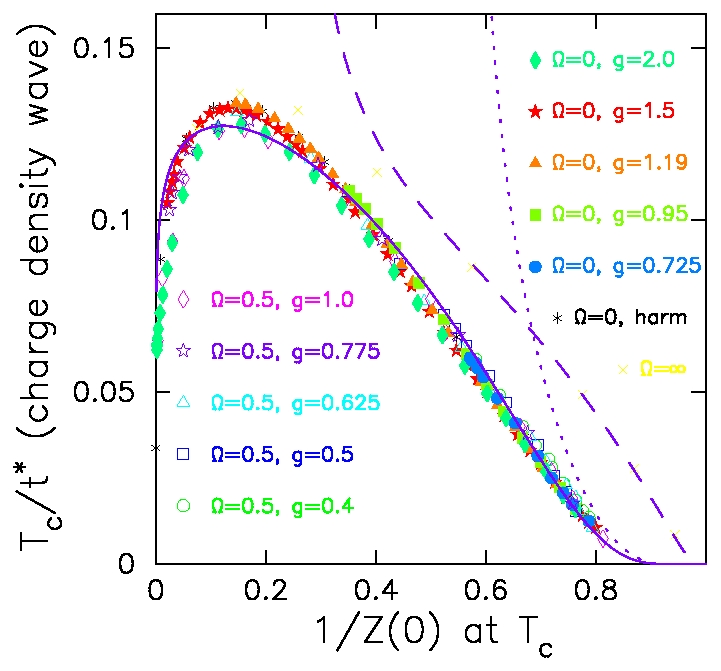• J. K. Freericks and V. Zlatic', Gap ratio in anharmonic charge-density-wave systems, Phys. Rev. B 64, 073109 (2001).
  J. K. Freericks, V. Zlatic', and M. Jarrell, Approximate scaling relation for the anharmonic electron-phonon problem, Phys. Rev. B 61, R838--841 (2000) (Rapid Communication).
  J. K. Freericks, M. Jarrell, and G. D. Mahan, The anharmonic electron-phonon problem, Phys. Rev. Lett. 77, 4588-4591 (1996); Erratum: Phys. Rev. Lett. 79, 1783 (1997).
  J. K. Freericks and G. D. Mahan, Strong-coupling expansions for the anharmonic Holstein model and for the Holstein-Hubbard model, Phys. Rev. B 54, 9372-9384 (1996); Erratum: Phys. Rev. B 56, 11321-11325 (1997).
  Here we examine differences that arise when anharmonic phonons interact with electrons (as one would normally expect to occur in a real material where the phonons are not harmonic since the lattice expands when heated). Surprisingly, we find scaling behavior of our results, which say that once one maps the anharmonic system onto an equivalent harmonic system, then both the single-particle and the two-particle properties are essentially the same for harmonic and anharmonic systems. This is surprising, because it requires scaling behavior for the transition temperature and the charge-density-wave gap at zero temperature, which one wouldn't naively expect to scale exactly the same way with anharmonicity.

  

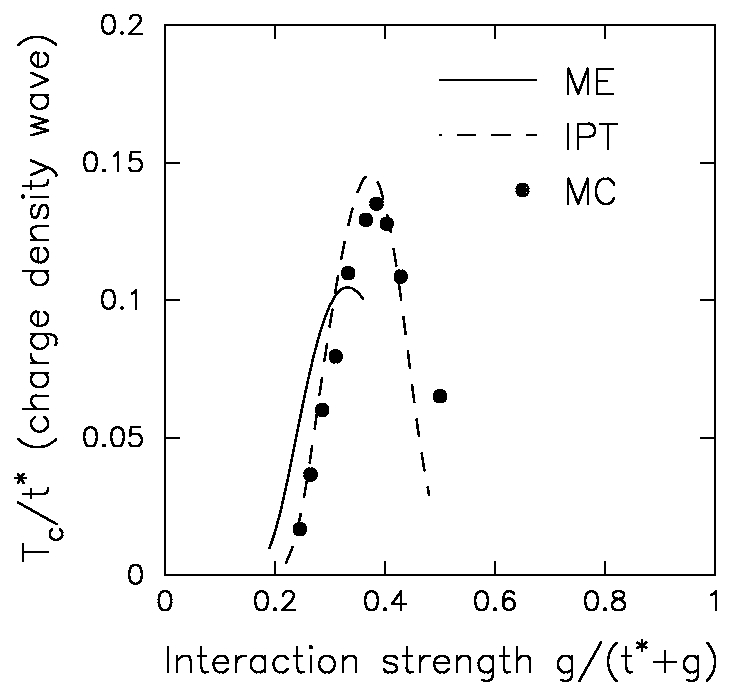
• P. Miller, J. K. Freericks, and E. J. Nicol, Possible experimentally observable effects of vertex corrections in superconductors, Phys. Rev. B 58, 14498--14510 (1998).
  J. K. Freericks, V. Zlatic', Woonki Chung, and M. Jarrell, Vertex-corrected perturbation theory for the electron-phonon problem with non-constant density of states, Phys. Rev. B 58, 11613--11623 (1998).
  J. K. Freericks and M. Jarrell, Iterated perturbation theory for the attractive Holstein and Hubbard models, Phys. Rev. B 50 , 6939-6953 (1994).
  J. K. Freericks, Conserving approximations for the attractive Holstein and Hubbard models, Phys. Rev. B 50, 403-417 (1994).
  J. K. Freericks and D. J. Scalap ino, Weak-coupling expansions for the attractive Holstein and Hubbard models, Phys. Rev. B 49, 6368-6371 (1994).
  E. J. Nicol and J. K. Freericks, Vertex corrections to the theory of superconductivity, Physica C 235-240, 2379-2380 (1994).
  J. K. Freericks, Strong-coupling expansions for the attractive Holstein and Hubbard models, Phys. Rev. B 48, 3881-3891 (1993).
  This is a series of weak and strong-coupling perturbation series expansions for the electron-phonon problem. We find that in the strong-coupling limit, the simple perturbative expansions are quite accurate when one is in the bipolaronic (pre-formed pair) regime. On the weak-coupling side, however, we find that virtually nothing allows you to accurately extend the conventional perturbation theory beyond a coupling strength on the order of one. We do predict, that the best way to look for effects of vertex corrections in a real material is through the isotope effect, which will have very different behavior if vertex corrections are important.



• J. K. Freericks and M. Jarrell, Competition between electron-phonon attraction and weak Coulomb repulsion, Phys. Rev. Lett., 75, 2570-2573 (1995).
  J. K. Freericks, M. Jarrell, and D. J. Scalapino, The electron-phonon problem in infinite dimensions, Europhys. Lett. 25, 37-42 (1994).
  J. K. Freericks and M. Jarrell, Simulation of the electron-phonon interaction in infinite dimensions, in Computer Simulations in Condensed Matter Physics VII, edited by D. P. Landau, K. K. Mon, and H.-B. Schuttler (Springer-Verlag, Heidelberg, Berlin, 1994).
  J. K. Freericks, M. Jarrell, and D. J. Scalapino, Holstein model in infinite dimensions, Phys. Rev. B 48, 6302-6314 (1993).
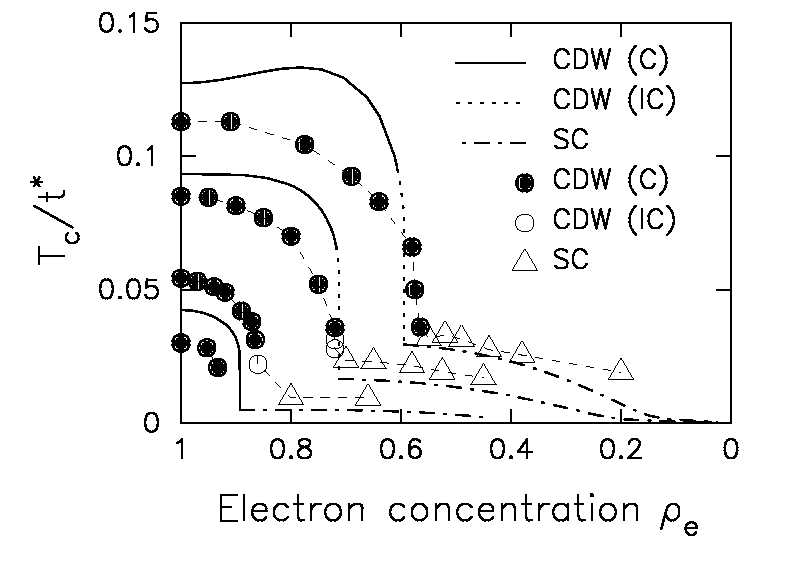
  This is a series of quantum Monte Carlo simulations investigating properties of harmonic electron-phonon systems and examining the regions of stability for charge-density-wave ordered phases versus superconductivity. A number of interesting results came out of this work ranging from unexpected robustness of the charge-density-wave order at half filling to a Coulomb repulsion, a change in character of the ground state from one that orders and pairs at Tc to one that has a preformed pair that condenses at a lower temperature, and a large reduction in transition temperatures due to vertex corrections.
• J. K. Freericks and E. H. Lieb, The ground state of a general electron-phonon Hamiltonian is a spin singlet, Phys. Rev. B 51 , 2812-2821 (1995).
  In this work, we show that the ground state of an electron-phonon system, with a wide range of different (nonlinear) couplings always contains a spin-singlet state. For a class of models (including the Holstein model), we show that the ground state is unique, and hence must be a spin singlet. One consequence of the uniqueness is that there is no self-trapping transition of a polaron, rather it is a smooth (albeit very rapid) transition from a delocalized to a localized ``quasiparticle.''

Bose Hubbard Model

• M. Niemeyer, J. K. Freericks, and H. Monien, Strong-coupling perturbation theory for the two-dimensional Bose-Hubbard model in a magnetic field, Phys. Rev. B 60 2357--2362 (1999).
  J. K. Freericks and H. Monien, Strong-coupling expansions for the pure and disordered Bose Hubbard model, Phys. Rev. B 53, 2691-2700 (1996).
  J. K. Freericks and H. Monien, Phase diagram of the Bose Hubbard model, Europhys. Lett. 26, 545-550 (1994).
  H. Monien and J. K. Freericks, Phase diagram of the Bose Hubbard model, in Strongly Correlated Electronic Materials Los Alamos Symposium 1993, edited by K. Bedell, E. Abrahams, A. Balatsky, D. Meltzer, and Z. Wang (Addison-Wesley, New York, 1994).
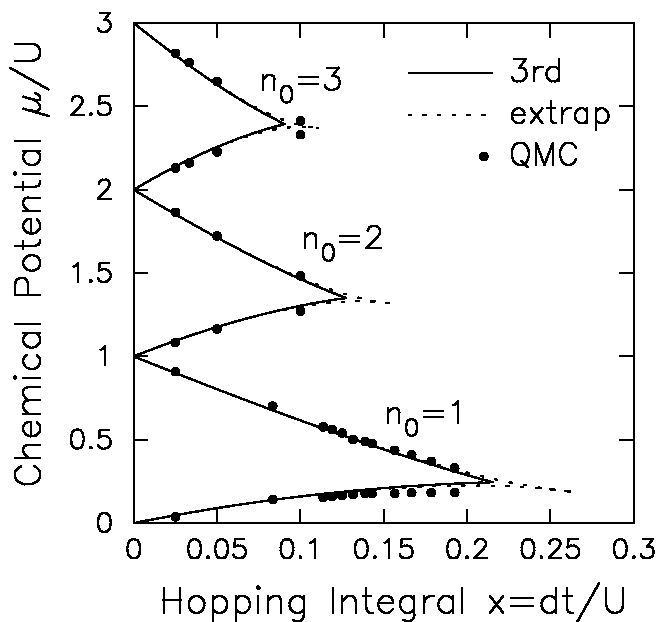
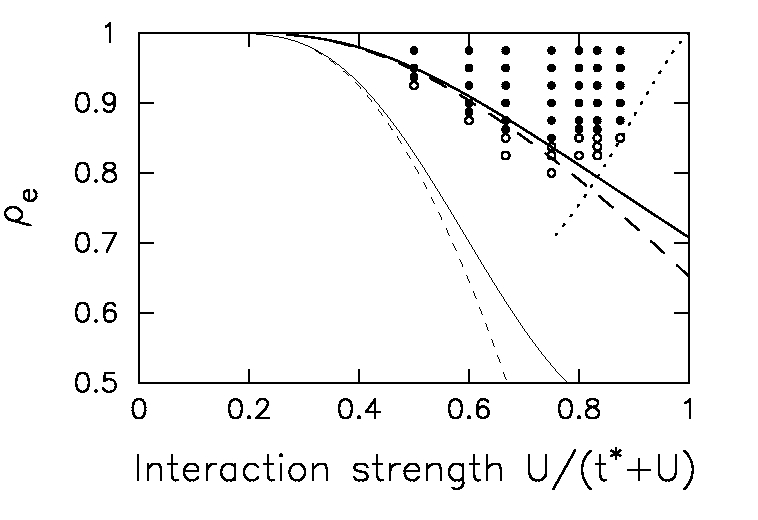
  This work focuses on using strong-coupling perturbation theory to determine the phase boundary of the bose Hubbard model, which can be viewed as a model for disordered superconductivity, where there is local pairing, but no global phase coherence. What is surprising in this work is that low-order perturbation theory can rival the accuracy of complicated quantum Monte Carlo simulations, and that one can determine phase boundaries in the disordered case much more accurately, because one can explicitly take into account so-called rare regions. Most of the results of this work was verified either numerically, by performing expansions to high order, or experimentally (by Mooij's group) on microfabricated Josephson junction array experiments.

Small Cluster Calculations

• J. K. Freericks and L. M. Falicov, Heavy-fermion systems in magnetic fields: the metamagnetic transition, Phys. Rev. B 46, 874-879 (1992).
  L. M. Falicov and J. K. Freericks, Electronic Structure of Highly Correlated Systems, in Condensed Matter Theories, Vol. 8, edited by L. Blum and F. Bary Malik (Plenum Press, 1992).
  J. K. Freericks, L. M. Falicov, and D. S. Rokhsar, Exact solutions of frustrated ordinary and chiral eight-site Hubbard models, Phys. Rev. B 44, 1458-1475 (1991).
  J. K. Freericks and L. M. Falicov, Exact many-body solution of the periodic-cluster t-t'-J model for cubic systems: ground-state properties, Phys. Rev. B 42, 4960-4978 (1990).
  This is work performed during my graduate-school days. We examined the exact solution of a number of Hubbard-like models on small clusters. Much interesting physics was discovered, especially about the stability of magnetic phases, and metamagnetism, but I found the finite-size effects were often too big to be able to make much progress with this approach.
• J. K. Freericks and L. M. Falicov, Enlarged symmetry groups of finite-size clusters with periodic boundary conditions, Lett. Math. Phys. 22, 277-285 (1991).
  J. K. Freericks and L. M. Falicov, Hidden symmetries of finite-size clusters with periodic boundary conditions, Phys. Rev. B 44, 2895-2904 (1991).
  These results, that finite-size clusters have extra symmetries, is something that I found to be fascinating when I discovered it to occur in a general case. Unfortunately, since the extra symmetry leads to ``accidental'' degeneracies in the many-body spectrum, this result also showed that until the cluster is large enough, finite-size effects can be very strong, and very difficult to disentangle, by any simple analysis of the calculated results.